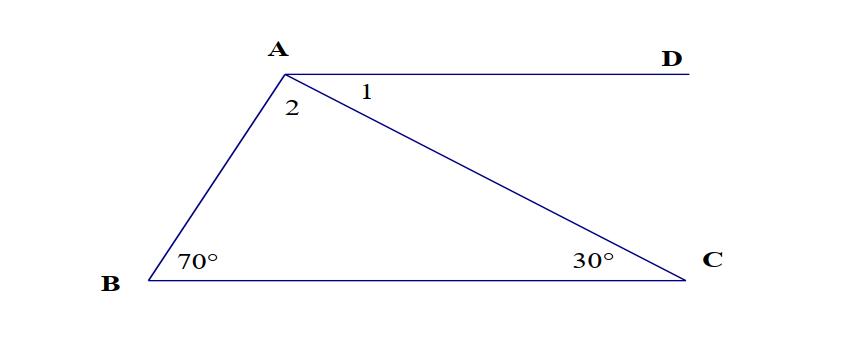
Cho tam giác ABC. B 70°, C 30° và đt AD song song với BC. Tính số đo a1 a2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A2.
N
30 tháng 9 2021
A1 = 30 độ ( Vì nó so e trong với acb và AD // BC )
A2 = 80 độ ( Tổng 3 góc trong tam giác nha bạn )
30 tháng 9 2021
Ta có: AD//BC
\(\Rightarrow\widehat{A_1}=\widehat{ACB}=30^0\)(so le trong)
Ta có: AD//BC
\(\Rightarrow\widehat{ABC}+\widehat{BAD}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{ABC}+\widehat{A_1}+\widehat{A_2}=180^0\)
\(\Rightarrow\widehat{A_2}=180^0-\widehat{ABC}-\widehat{A_1}=180^0-70^0-30^0=80^0\)
10 tháng 9 2021
\(a,\widehat{A}+\widehat{B}+\widehat{C}=180\\ \Rightarrow180-3\widehat{C}+\widehat{C}+70=180\\ \Rightarrow-2\widehat{C}=-70\\ \Rightarrow\widehat{C}=35\\ \Rightarrow\widehat{A}=180-35=145\)
5 tháng 9 2017
a, Vì Dx // BC nên: xDC = ACB (hai góc so le trong)
\(\Rightarrow\)ACB=70o.
Xét tam giác ABC có:
ACB+ABC+BAC=180o(tổng ba góc trong một tam giác)
\(\Rightarrow\)ABC=180o-70o-40o=70o.
Vậy ACB=70o; ABC=70o.
b, Ta có:
DAB+BAC=180o (hai góc kề bù).
DAB=180o-40o=140o.
Vì Ay là phân giác của DAB nên DAy = yAB=\(\dfrac{140^o}{2}\)=70o.
\(\Rightarrow\)yAB=ABC=70o. Mà hai góc này ở vị trí so le trong nên Ay // BC.
c,Theo bài, Am là phân giác của BAC nên: BAm = CAm = 20o.
Bn là phân giác của ABC nên: ABn = CBn = 35o.
Mà BEm là góc ngoài tại đỉnh E của tam giác ABE nên:
BEm =35o+20o=55o
T
17 tháng 8 2018
Bài giải :
a, Vì Dx // BC nên: xDC = ACB (hai góc so le trong)
⇒ACB=70o.
Xét tam giác ABC có:
ACB+ABC+BAC=180o(tổng ba góc trong một tam giác)
⇒ABC=180o-70o-40o=70o.
Vậy ACB=70o; ABC=70o.
b, Ta có:
DAB+BAC=180o (hai góc kề bù).
DAB=180o-40o=140o.
Vì Ay là phân giác của DAB nên DAy = yAB=140°/2 =70o.
⇒yAB=ABC=70o. Mà hai góc này ở vị trí so le trong nên Ay // BC.
c,Theo bài, Am là phân giác của BAC nên: BAm = CAm = 20o.
Bn là phân giác của ABC nên: ABn = CBn = 35o.
Mà BEm là góc ngoài tại đỉnh E của tam giác ABE nên:
BEm =35o+20o=55o
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
Vì $\widehat{BAC}=60^0$ và $AD$ là tia phân giác $\widehat{A}$ nên $\widehat{BAD}=\frac{1}{2}\widehat{BAC}=30^0$
Theo hình vẽ $Bx\parallel AD$ nên $\widehat{ABx}=\widehat{BAD}=30^0$ (hai góc so le trong)
$\widehat{ABy}=180^0-\widehat{ABx}=180^0-30^0=150^0$