Cho tam giác ABC vuông tại A,M là trung điểm của BC. Chứng minh rằng AM =1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DG
0
HD
1
19 tháng 1 2017
vẽ thêm MD song song AH
MH song song AD
Xét tam giác MDA và tam giác AHM có
Góc A1 = góc M2 (so le trong)
Góc A2 = góc M1 ( so le trong)
AM là cạnh chung
\(\Rightarrow\)Tam giác MDA = tam giác AHM (g.c.g)
\(\Rightarrow\)MD = AH (2 cạnh tương ứng)
Xét tam giác MBD và tam giác CMH có
Góc BMD = góc MCH (đồng vị)
Góc D1 = góc H2 (=90)
BM = MC (giả thiết)
\(\Rightarrow\)Tam giác MBD = tam giác CMH (cạnh huyền - góc nhọn)
\(\Rightarrow\)BD = MH ( 2 cạnh tương ứng)
Xét tam giác BDM và tam giác MHA có
MD = AH ( cmt)
Góc D2 = góc H1 (=90)
BD = MH (cmt)
\(\Rightarrow\)tam giác MBD = tam giác MAH ( c.g.c)
\(\Rightarrow\)BM = AM (2 cạnh tương ứng)
Vì BM = MC và AM = BM
\(\Rightarrow\)AM = MC
Mà BC = BM + MC
\(\Rightarrow\)BC = 2*AM
\(\Rightarrow\)AM = \(\frac{1}{2}\cdot BC\)
Vậy AM = \(\frac{1}{2}\cdot BC\)
KV
25 tháng 5 2023
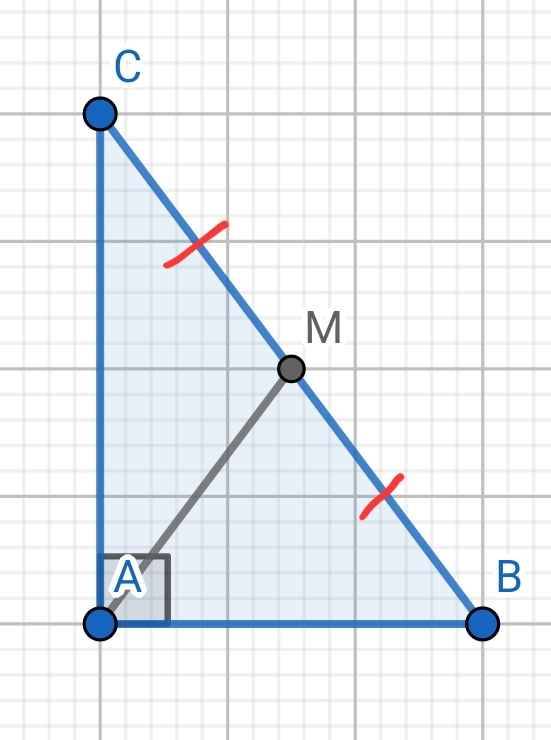
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2
TH
0
26 tháng 8 2021
Trên tia đối của tia MA, lấy điểm D sao cho MA=MD
Xét tứ giác ACDB có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ACDB là hình bình hành
Hình bình hành ACDB có \(\widehat{CAB}=90^0\)
nên ACDB là hình chữ nhật
Suy ra: BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
CL
0
A B C M N
∆ABC có M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm N sao cho MN = MA.
Ta có:
ےAMB = ےNMC (đối đỉnh)
BM = CM (giả thiết)
MA = MN (dựng hình)
Suy ra: ∆MAB = ∆MNC (c.g.c)
Suy ra: NC = AB và ےMBA = ےMCN
Do ےMBA = ےMCN nên AB // NC
Suy ra ےBAC + ےACN = 180
Ta có: ےBAC = 90 nên ےACN = 90
=> ∆ABC = ∆CNA (c.g.c) vì AC là cạnh chung
AB = NC (cmt) và ےBAC = ےACN = 90
=> AN = BC
=> AM = \(\frac{1}{2}BC\)
=>CMT
Ta có: tam giác ABC vuông tại A,M là trung điểm của BC (gt) => AM là đg trung tuyến ứng vs cạnh huyền BC của tam giác vuông ABC
=>AM = 1/2 BC ( trong tam giác vuông, đg trung tuyến ứng vs cạnh huyền bằng nửa cạnh huyền )
Vậy....