Tính A = 1 + 4 + 42 + 43 + ... +4n ( n > 2 , n thuộc N)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
29 tháng 10 2016
dùng đồng dư
a)\(3^{4n+1}=3^{4n}.3=\left(3^4\right)^n.3=81^n.3\)
81 đồng dư với 1 (mod2)
=>81n đồng dư với 1 (mod2)
=>81n.3 đồng dư với 3 (mod2)
=>81n.3 chia 2 dư 3 hay 34n+1 ko chia hết cho 2
Tương tự 34n+1 cùng ko chia hết cho 5,10
các câu còn lại tương tự
NT
2
10 tháng 11 2016
Nếu n chẵn thì cái tổng chia hết cho 2
Nếu n lẻ thì
Phân tích nhân tử
Ta có : \(n^4+4^n=\left(n^2\right)^2+\left(2^n\right)^2+2n^2+2^n=\left(n^2+2^n\right)^2-n^2+2^{n+1}=\left(n^2+2^n-n.2^{\frac{n+1}{2}}\right)\left(n^2+2^n+n.2^{\frac{n+1}{2}}\right)\)
Ta chỉ cần chứng minh cả 2 thừa số đều lớn hơn 1 là được
Tức là ta chứng minh \(n^2+2^n-n.2^{\frac{n+1}{2}}\ge1\)
Tương đương với \(n^2+2^{n+1}-2n.2^{\frac{n+1}{2}}+n^2\ge2\) ( nhân 2 cho 2 vế )
\(BĐT\Rightarrow\left(n-2^{\frac{n+1}{2}}\right)^2+n^2\ge2\)đúng với n lẻ và n ≥ 3
Vậy, ta có điều phải chứng minh
NM
2
6 tháng 10 2021
\(3^{8n+2}+2^{12n+3}\)
\(=24^n\cdot9+24^n\cdot8\)
\(=24^n\cdot17⋮17\)
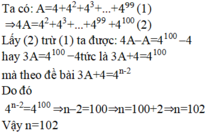
4a=4+4^2+4^3+.......+4^n+1
4a-a=(......)-(......)
3a=4^n+1-1
a=4^n+1-1/3