cho tam giác ABC có 3 góc nhọn. gọi O là trung điểm của BC. gọi D là điểm đối xứng của A qua BC; E là điểm đối xứng của A qua O. cmr: BCED là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 8 2017
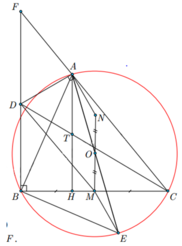
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
21 tháng 10 2021
a. Chứng minh tứ giác BHCD là hình bình hành
b. Chứng minh các tam giác ABD vuông tại B, ACD vuông tại C
10 tháng 11 2021
mình đag kt á nên bạn giải vẽ hình dùm mình đc hongg
25 tháng 2 2022
1
a) ta có A đối xứng với F qua O => O là trung điểm của AF
=> BO là trung tuyến của AF (1)
=> CO là trung tuyến của AF (2)
ta lại có O là giao điểm của 3 đường trung trực của tam giác ABC
=> OA = OB =OC (3)
từ 1-2-3 => Góc ABF = góc ACF = 90
=> AB vuông góc với FB
AC vuông góc với FC
mà CH vuông góc AB => CH // BF
BH vuông góc với AC => BH//CF
Xét tứ giác BHCF có
CH // BF
BH//CF
=> HBFC là hình bình hành (dhnb) có HF và BC là 2 đường chéo
M là trung điểm của BC
=> M là trung điểm của HF => 3 điểm H,M,F thẳng hàng ; HM =FM
=> H đối xứng với F qua M
b) Xét tam giác AHF có M là trung điểm của HF O là trung điểm AF
=> OM là đường trung bình
=> OM =1/2AH <=> AH/OM=2
vì H là giao điểm của 2 đường cao BD và CE nên H là trực tâm => AH vuông góc BC
ta lại có OM vuông góc với BC ( M là trung điểm của BC ; O là giao 3 đường trung tuyến => OM là đường trung tuyến của BC )
=> OM // AH => góc HAG =góc GMO (2 góc so le trong)
xét tam giác AHG và tam giác MOG
có :góc HGA =góc MGO (2 góc đối đỉnh)
góc HAG =góc GMO (cmt)
=> đồng dạng (gg) => AH /OM = AG/MG =2
<=> AG=2MG <=> AM = AG + MG =3MG
<=> AG/AM =2/3 mà AM là tiếp tuyến của BC ( m là trnug điểm BC)
=> G là trọng tâm của tma giác ABC
Ta có : A đối xứng D qua BC , gọi AD cắt BC tại H ta có AD \(\perp\) BC tại H và AH = HD
Xét tg ADE ta có ; AH = HD , AO = OE
=> OH // DE hay BC // DE .
tứ giác BCED có BC//DE => BCED là hih thang .
Xét tg OAB và tg OEC có :
OB = OC , OA = OE , góc AOB = góc COE
=> tg OAB = tg OEC => góc ABO = góc OCE (1).
Có : BH \(\perp\) AD tại trung điểm H của AD
=> BAD cân tại B => góc ABH = góc HBD (2) .
Từ (1) và (2) có : góc HBD = góc OCE
=> hih thang BCED có : góc HBD = góc OCE
=> BCED là hih thang cân .
A B D E C O H