Tìm x
5x(x-2) +2-x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
(x+3)(5x+10)=0
x=-3 hoặc x=-2
Vậy \(x\in\left\{-3;-2\right\}\)
NL
1
9 tháng 8 2021
Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
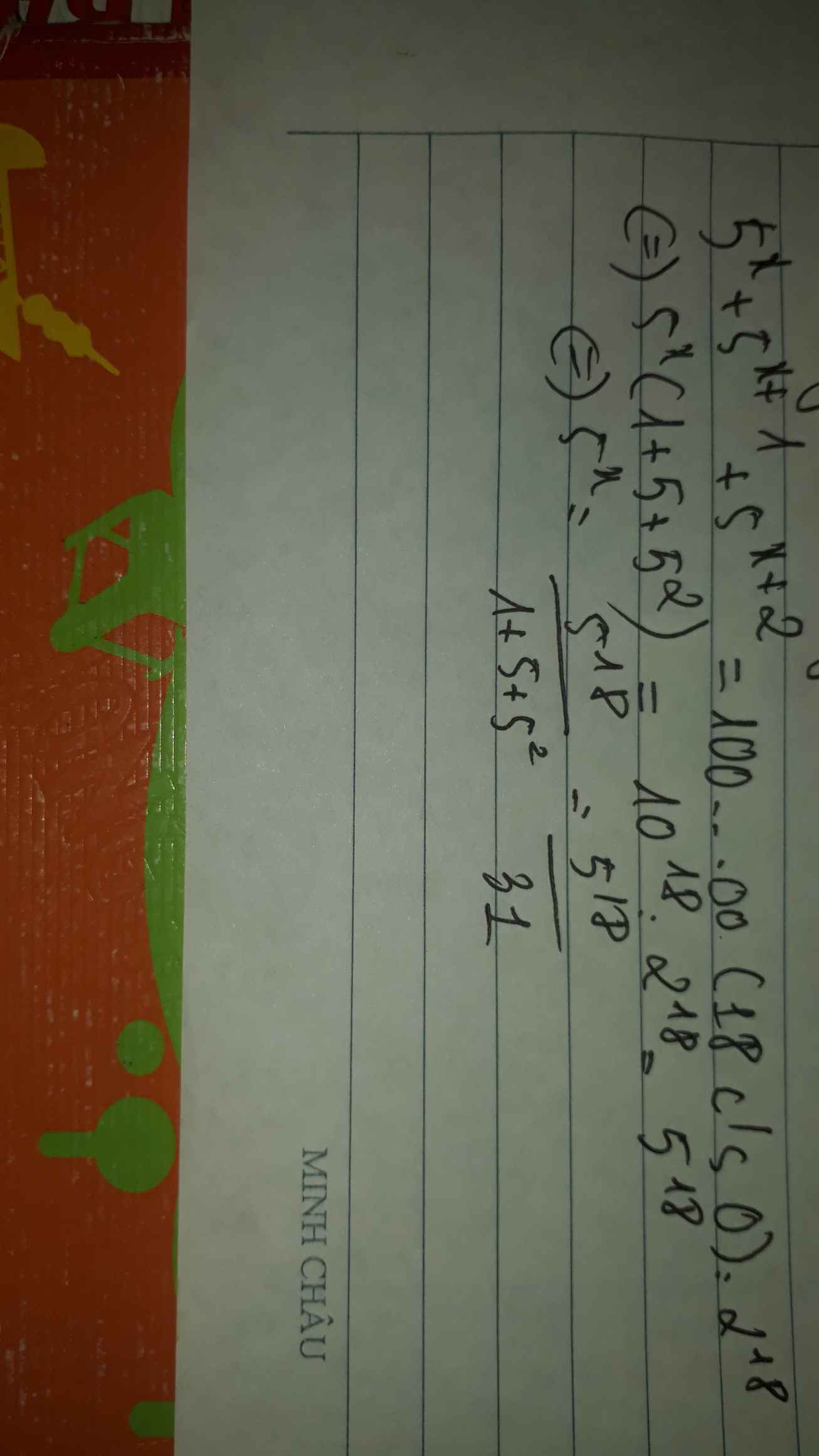
Nếu là dấu nhân thì ta có:
8 tháng 10 2021
a) \(5x\left(x-7\right)-30\cdot\left(x-7\right)=0\)
\(\Rightarrow\left(5x-30\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5x-30=0\\x-7=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=6\\x=7\end{matrix}\right.\)
b) \(\left(2x-4\right)\left(2x+4\right)-x\left(x+3\right)=3x\left(x+5\right)\)
\(\Rightarrow4x^2-16-x^2-3x=3x^2+15x\)
\(\Rightarrow-16=18x\Rightarrow x=-\dfrac{8}{9}\)
4 tháng 4 2022
d. Áp dụng BĐT Caushy Schwartz ta có:
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}\le x+y+\dfrac{\left(1+1\right)^2}{x+y}=x+y+\dfrac{4}{x+y}\le1+\dfrac{4}{1}=5\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
L
27 tháng 11 2019
1)Tìm x
a) (x+1)(x-2)<0
=>Có 2TH:
TH1:
x+1<0=>x< -1
x-2>0=>x>2
=>Vô lí
TH2:
x+1>0=>x> -1
x-2<0=>x<2
=> -1<x<2
Vậy x thuộc {0;1}
b) Tương tự a thôi ạ.
c) (x-2)(3x+2)
=> Có hai TH:
TH1:
x-2<0=>x<2
3x+2<0=>3x< -2=>x< -2/3
=>x< -2/3
TH2:
x-2>0=>x>2
3x+2>0=>3x> -2=>x> -2/3
=>x>2
Vậy x< -2/3 hoặc x>2
2)Tìm x
x.x=x
<=>x²-x=0
<=>x(x-1)=0
<=>x=0 hoặc x=1
HP
5 tháng 1 2021
1.
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta=25-12m>0\\x_1^2+x_2^2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(x_1+x_2\right)^2-2x_1x_2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(2m-3\right)^2-2\left(m^2-4\right)< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\2m^2-12m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \dfrac{25}{12}\)
\(5x\left(x-2\right)+2-x=0\)
\(5x\left(x-2\right)+\left(2-x\right)=0\)
\(5x\left(x-2\right)-\left(x-2\right)=0\)
\(\left(x-2\right)\left(5x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-2=0\\5x-1=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{1}{5}\end{cases}}\)
Vậy,.......
5x(x-2)-(x-2)=0
(x-2)(5x-1)=0
\(\orbr{\orbr{\begin{cases}x-2=0\\5x-1=0\end{cases}}}\orbr{\begin{cases}x=0\\5x=1\end{cases}}\orbr{\begin{cases}x=0\\x=\frac{1}{5}\end{cases}}\)