cho hình vẽ , hãy cm AI // BJ biết A đối xứng S1 , B đối xứng S2
M S1 S2 N I B A J
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2019
Chọn C.
Diện tích toàn phần của hình lập phương là
Hình trụ có bán kính đáy là 20 cm và đường cao là 40 cm nên diện tích toàn phần của hình trụ là
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2021
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
CM
24 tháng 5 2017
Chọn D.
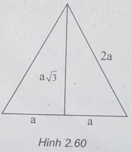
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
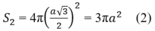
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1