Question

[Ryoji]

tìm a , b , c của đồ thị hàm số y= ax² +bx +c biêt đồ thị hàm số đi qua A (-2;7) , B(3;2) , giá trị nhỏ nhất là -2

Answer 1

[Ngô Thị Phương Anh]

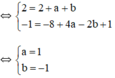
Vì đồ thị hàm số đi qua điểm A(-2;7) nên ta có:

4a-2b+c=7 (1)

Vì đồ thị hàm số đi qua điểm B(3;2) nên ta có:

4a+2b+c=2 (2)

Giá trị nhỏ nhất là -2 => \(\dfrac {-b^2+4ac}{4a}\)=-2

<=>-8a+\(b^2\)-4ac=0 (3) (a khác 0)

Lấy (1) trừ (2) ta có:

b= \(\dfrac {-5}{4}\) thay vào (1) ta có:

(1) 4a+\(\dfrac {5}{2}\)+c=7

<=>4a+c=4.5

<=> c=4.5-4a

thay b và c vừa tìm vào (3) ta có:

\(16a^2 \) -26a+\(\dfrac {25}{16}\) =0

=> a=25/16

hoặc a=1/16

=> c =13/4

hoặc a=37/4