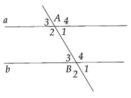
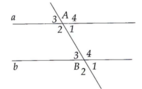
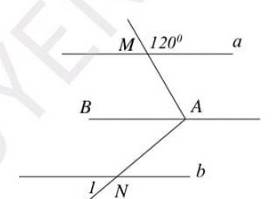
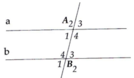
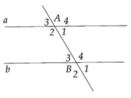
Trên hình trên cho biết a// b . Tính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 5 2017
Tương tự 5. Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °
CM
5 tháng 10 2018
Tính được A 3 ^ = A 1 ^ = B 3 ^ = B 1 ^ = 60 ° A 2 ^ = A 4 ^ = B 2 ^ = B 4 ^ = 120 °
DH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 8 2023
\(\widehat{BAM}\) = 1800 - 1200 = 600
\(\widehat{BAN}\) = 1000 - 600 = 400
⇒ N1 = \(\widehat{BAN}\) = 400( hai góc đồng vị)
CM
17 tháng 1 2017
Ta có a //b nên B 1 ^ = A 1 ^ = 75° (hai góc đồng vị).
A 3 ^ = A 1 ^ = 75 ° ; B 3 ^ = B 1 ^ =75° (cặp góc đối đỉnh).
Lại có A 1 ^ + A 2 ^ = 180 ° (hai góc kề bù)
=> A 2 ^ = 180°- 75° = 105°.
B 4 ^ = A 2 ^ = 105° (hai góc đồng vị)
B 4 ^ = B 2 ^ = 105°; A 4 ^ = A 2 ^ = 105° (cặp góc đối đỉnh)
22 tháng 5 2023
Gọi $S_{MNB}$ là diện tích tam giác $MNB$, $x$ là diện tích tam giác $MPN$.
Ta có $MB = CA$, suy ra $S_{MNB} = S_{MCA}$.
Gọi $h$ là độ cao của tam giác $MPN$ từ đỉnh $P$. Ta có:
$$\frac{AP}{AN} = \frac{1}{3} \Rightarrow \frac{PN}{AN} = \frac{2}{3} \Rightarrow \frac{h}{MA} = \frac{2}{3} \Rightarrow h = \frac{2}{3} MA$$
Do $MB = CA$, suy ra $S_{MNB} = S_{MCA} = \frac{1}{2} MB \cdot h = \frac{1}{2} CA \cdot h$.
Mà $MB + CA = MA$, suy ra $S_{MNB} + S_{MCA} = \frac{1}{2} MA \cdot h$.
Từ đó, ta có:
$$2S_{MNB} = \frac{1}{2} MA \cdot h - S_{MNB} = \frac{1}{2} S_{MPN}$$
$$\Rightarrow S_{MPN} = 4S_{MNB} = 4 \cdot 13 = 52 \text{ (cm}^2\text{)}$$
Vậy diện tích tam giác $MPN$ là 52 cm$^2$.