Cho hàm số f(x)=x2-5x+6
Tìm x để: f(x)=12 và f(x)=20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 12 2019
Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có 
Đặt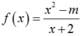 
khi x < 3 (m là tham số, m > 0).
Ta có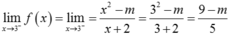 
.
Để hàm số f(x) có giới hạn khi x → 3 thì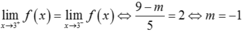 
.
CM
12 tháng 7 2018
F(x) là một nguyên hàm của hàm số f(x) => F'(x) = f(x)
Đồng nhất ta được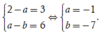 
Chọn B.
CM
1 tháng 6 2019
Đáp án B
Ta có F x = x 2 + a x + b e - x ⇒ F ' x = - x 2 + 2 - a x + a - b e - x
mà f x = F ' x suy ra - x 2 + 2 - a x + a - b = - x 2 + 3 x + 6 ⇒ 2 - a = 3 a - b = 6 ⇔ a = - 1 b = - 7
CM
29 tháng 8 2019
Chọn D
Từ giả thiết ta có:
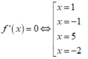
Từ bảng biến thiên ta thấy f'(x) đổi dấu tại x = -2 và x = 5 do đó hàm số f(x) có 2 điểm cực trị.
\(f\left(x\right)=12\Rightarrow x^2-5x+6=12\Rightarrow x^2-5x-6=0\)
\(\Rightarrow x^2+x-6x-6=0\Rightarrow x\left(x+1\right)-6\left(x+1\right)=0\)
\(\Rightarrow\left(x-6\right)\left(x+1\right)=0\Rightarrow\orbr{\begin{cases}x=6\\x=-1\end{cases}}\)
\(f\left(x\right)=20\Rightarrow x^2-5x+6-20=0\Rightarrow x^2-5x-14=0\)
\(\Rightarrow x^2+2x-7x-14=0\)
\(\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\orbr{\begin{cases}x=7\\x=-2\end{cases}}\)