Giải câu g,h,i,k,l,m thôi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
27 tháng 6 2020
Bài 2 :
- Ta có : \(R=\frac{1}{2}\) đường chéo = \(\frac{1}{2}\) cạnh huyền .
=> Cạn huyền là 5.2 = 10 cm .
=> Diện tích hình chữ nhật đó là : xy = 6.8 = 48 ( cm2 )
Vây ...
27 tháng 6 2020
Bài 1 :
- Gọi cạnh góc vuông lớn là x,cạnh góc vuông nhỏ là y ( cm, x > y > 0 )
Theo đề bài hiệu hai cạnh góc vuông là 2 cm nên ta có phương trình :
x - y =2 ( I )
- Áp dụng định lý pi ta goc vào tam giác trên ta được :
CGV2 + CGV2 = CH2 .,
=> \(x^2+y^2=10^2=100\left(II\right)\)
- Từ ( I ) và ( II ) ta có hệ phương trình : \(\left\{{}\begin{matrix}x-y=2\\x^2+y^2=100\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=x-2\\x^2+\left(x-2\right)^2=100\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=x-2\\x^2+x^2-4x+4=100\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=x-2\\2x^2-4x-96=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}y=x-2\\\left[{}\begin{matrix}x=8\left(TM\right)\\x=-6\left(L\right)\end{matrix}\right.\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=8\\y=6\end{matrix}\right.\) ( TM )
Vậy độ dài hai cạnh góc vuông lần lượt là 8, 6 cm .
KV
18 tháng 8 2023
c) A = x.M + (4x + 7)/(√x + 3)
= 3x/(√x + 3) + (4x + 7)/(√x + 3)
= (7x + 7)/(√x + 3)
Để A nhỏ nhất thì 7x + 7 nhỏ nhất
Mà x ≥ 0
⇒ 7x + 7 ≥ 7
⇒ GTNN của A là 7/3 khi x = 0
2 tháng 5 2020
Câu 54:
a) Xét tứ giác AHDK có
\(\widehat{KAH}=90^0\)(\(\widehat{BAC}=90^0\),K∈AC, H∈AB)
\(\widehat{AHD}=90^0\)(DH⊥AB)
\(\widehat{AKD}=90^0\)(DK⊥AC)
Do đó: AHDK là hình chữ nhật(dấu hiệu nhận biết hình chữ nhật)
b)
Ta có: AHDK là hình chữ nhật(cmt)
⇒DK//AH(hai cạnh đối trong hình chữ nhật AHDK)
Xét ΔABC có
D là trung điểm của BC(gt)
DK//AB(DK//AH, B∈AH)
Do đó: K là trung điểm của AC(định lí 1 về đường trung bình của tam giác)
Xét tứ giác AICD có
K là trung điểm của đường chéo ID(I và D đối xứng nhau qua K)
K là trung điểm của đường chéo AC(cmt)
Do đó: AICD là hình bình hành(dấu hiệu nhận biết hình bình hành)
Xét hình bình AICD có ID⊥AC(DK⊥AC, I∈DK)
nên AICD là hình thoi(dấu hiệu nhận biết hình thoi)
c) Để hình chữ nhật AHDK trở thành hình vuông thì AD là tia phân giác của \(\widehat{KAH}\)
hay AD là tia phân giác của \(\widehat{BAC}\)
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(D là trung điểm của BC)
AD là đường phân giác ứng với cạnh BC(cmt)
Do đó: ΔABC cân tại A(định lí tam giác cân)
hay AB=AC
Vậy: Khi ΔABC có thêm điều kiện AB=AC thì AHDK trở thành hình vuông
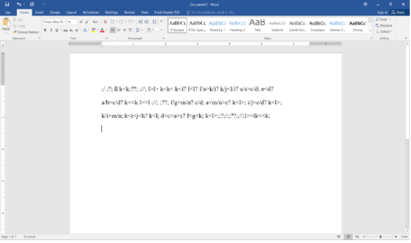
Câu g,h,i,k,l,m của bài 1 hay bài 2 ấy bạn?
Bài 2 ạ