giải phương trình
( 2x2 -x -1) - 3 = 4x2 - 2x + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 3 2019
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
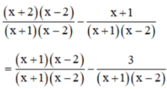
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
CM
26 tháng 6 2017
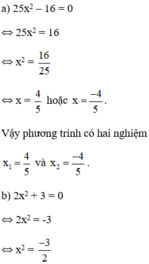
Phương trình vô nghiệm vì x 2 ≥ 0 với mọi x.
c) 4 , 2 x 2 + 5 , 46 x = 0
⇔ x.(4,2x + 5,46) = 0
⇔ x = 0 hoặc 4,2x + 5,46 = 0
+Nếu 4,2x + 5,46 = 0 ⇔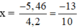 
Vậy phương trình có hai nghiệm
x
1
=
0
và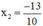 
d) 4 x 2 - 2 √ 3 x = 1 - √ 3 . ⇔ 4 x 2 - 2 √ 3 x – 1 + √ 3 = 0
Có a = 4; b’ = -√3; c = -1 + √3;
Δ ’ = b ' 2 – a c = ( - √ 3 ) 2 – 4 ( - 1 + √ 3 ) = 7 - 4 √ 3 = 4 – 2 . 2 . √ 3 + ( √ 3 ) 2 = ( 2 - √ 3 ) 2 .
Phương trình có hai nghiệm phân biệt:
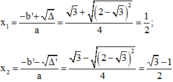
Cách 2: Sử dụng công thức nghiệm thu gọn với a, b, c
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt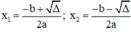 
+ Nếu Δ = 0, phương trình có nghiệm kép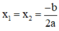 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
\(\left(2x^2-x-1\right)-3=4x^2-2x+2\)
\(\Leftrightarrow2x^2-x-1-3-4x^2+2x-2=0\)
\(\Leftrightarrow-2x^2+x-6=0\)
\(\Leftrightarrow-2\left(x^2-\dfrac{x}{2}+3\right)=0\)
\(\Leftrightarrow-2\left(x^2-2.x.\dfrac{1}{4}+\dfrac{1}{16}\right)-\dfrac{47}{8}=0\)
\(\Leftrightarrow-2\left(x-\dfrac{1}{4}\right)^2-\dfrac{47}{2}=0\left(l\right)\)
Vậy ptvn!