So sánh 5090 với 33.2205.Hãy chứng minh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Trên tia AC, AB' = AB
mà AB < AC ( giả thiết)
nên B' nằm giữa hai tia BA và BC
=> tia BB' nằm giữa hai tia BA và BC
=> ˆABB′<ˆABCABB′^<ABC^
b) ∆ABB' có AB = AB' nên cân tại A
=> ˆABB′<ˆAB′BABB′^<AB′B^
c) Vì là góc ngoài tại B' của ∆BB'C nên ˆABB′<ˆACBABB′^<ACB^
Vì ˆABB′<ˆABCABB′^<ABC^ (câu a)
ˆABB′<ˆAB′BABB′^<AB′B^ (câu b)
ˆAB

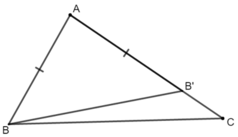
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
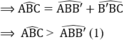

a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)