Có m+1/m=4.Tìm giá trị của m4+1/m4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 5 2018
Chọn A
y ' = y = 4 x 3 - 4 m 2 x
Hàm số có 3 điểm cực trị khi m ≠ 0
Khi đó 3 điểm cực trị là
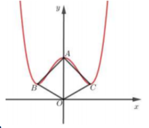
Gọi I là tâm đường tròn ngoại tiếp( nếu có) của tứ giác ABOC .
Do tính chất đối xứng , ta có
A,O,I thẳng hàng
⇒ A O là đường kính của đường tròn ngoại tiếp( nếu có) của tứ giác ABOC
Kết hợp điều kiện m = ± 1 ( thỏa mãn)
CM
16 tháng 4 2019
Phương pháp:
+) Tìm tọa độ các điểm cực trị của đồ thị hàm số theo tham số m.
+) Dựa vào tính chất hàm trùng phương và tính chất tứ giác nội tiếp để tìm m.
Cách giải:
CM
30 tháng 10 2018
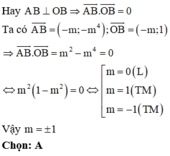
Chọn C
Hàm số có 3 cực trị ⇔ m > 0
Khi đó 3 điểm cực trị của đồ thị hàm số là
Do tính chất đối xứng, ta có ∆ A B C cân tại đỉnh A
Vậy ∆ A B C đều chỉ cần AB = BC
Kết hợp điều kiện ta có m = 3 3 (thỏa mãn)
Lưu ý: có thể sử dụng công thức b 3 8 a + 3 = 0
( - 2 m ) 3 8 + 3 = 0 ⇔ m 3 = 3 m ⇔ m = 3 3
CM
6 tháng 9 2018
Đáp án A
Xét hàm số y = x 4 − 2 m x 2 + 2 m + m 4 , có y ' = 4 x 3 − 4 m x , ∀ x ∈ ℝ
Phương trình y ' = 0 ⇔ 4 x 3 − 4 m x = 0 ⇔ x x 2 − m = 0 ⇔ x = 0 x 2 = m *
Để hàm số có ba điểm cực trị ⇔ * có 2 nghiệm phân biệt khác 0
Khi đó, gọi A 0 ; 2 m + m 4 , B m ; m 4 − m 2 + 2 m , C − m ; m 4 − m 2 + 2 m là tọa độ ba điểm cực trị của đồ thị hàm số.
Tam giác ABC đều ⇔ A B 2 = B C 2 ⇔ m + m 4 = 4 m ⇔ m 4 = 3 m ⇔ m = 3 3
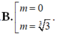
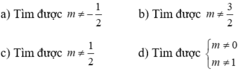
\(\frac{m+1}{m}=4\Rightarrow1+\frac{1}{m}=4\Leftrightarrow\frac{1}{x}=3\)
\(\Rightarrow\frac{1}{x^4}=3^4=81\)
\(\Rightarrow\frac{m^4+1}{m^4}=1+\frac{1}{m^4}=1+81=82\)
Ta có: \(m+\frac{1}{m}=4\)
<=> \(\left(m+\frac{1}{m}\right)^2=16\)
<=> \(m^2+\frac{1}{m^2}+2=16\)
<=> \(m^2+\frac{1}{m^2}=14\)
=> \( \left(m^2+\frac{1}{m^2}\right)^2=196\)
<=> \(m^4+\frac{1}{m^4}+2=196\)
<=> \(m^4+\frac{1}{m^4}=194\)
p/s: chúc bạn học tốt