Lập bảng xét dấu:
\(\dfrac{10}{x^2+2x+1}\)> 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
0
T
2
12 tháng 9 2015
Ta có: (x-3)(x+4)>0
=>hoặc x-3>0 nên x>3
x+4>0 nên x>-4
nên x>3
=>hoặc x-3<0 nên x<3
x+4<0 nên x<-4
nên x<-4
Vậy hoặc x>3 hoặc x<-4 thì (x-3)(x+4)>0
LT
12 tháng 9 2015
Lập bảng xét dấu:
| x | -4 | 3 |
| x-3 | - I - | - 0 + |
| x+4 | - 0 + | + I + |
| (x-3).(x+4) | + 0 - | - 0 + |
Để (x-3).(x+4) > 0 <=> x<-4 hoặc x>3
26 tháng 1 2016
bạn ấn vào đúng 0 sẽ ra đáp án, mình giải bài này rồi
31 tháng 8 2016
\(\left(x-2\right)\left(2x+3\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\) và \(\left(2x+3\right)\) trái dấu .
Mà : \(\left(2x+3\right)>\left(x-2\right)\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x+3>0\\x-2< 0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x>\frac{-3}{2}\\x< 2\end{array}\right.\)
\(\Leftrightarrow\frac{-3}{2}< x< 2\)
CM
7 tháng 11 2019
f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
+ Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0
Do đó 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2
+ Tam thức –8x2 + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên luôn mang dấu –.
+ Nhị thức 2x + 9 có nghiệm x = –9/2.
Ta có bảng xét dấu:
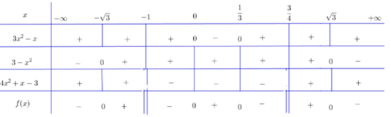
Kết luận:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
NL
2
25 tháng 9 2015
Đặt A = (x-2)2.(x+1/3).(x-1)
Ta có bảng xét dấu :
| x | \(-\frac{1}{3}\) | 1 | 2 | |||
| (x-2)2 | + | + | + | + | + | 0 |
| x + \(\frac{1}{3}\) | + | 0 | - | + | + | + |
| x - 1 | - | - | - | 0 | + | + |
| A | - | 0 | + | 0 | + | 0 |
Vậy để A < 0 <=> x < \(-\frac{1}{3}\)
\(\dfrac{10}{x^2+2x+1}>0\)
Ta có: \(\dfrac{10}{x^2+2x+1}=\dfrac{10}{\left(x+1\right)^2}>0\) với mọi x ≠ -1