Cho a-2b=5 và ab = 4 . Tính P = a2 + 4b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
4 tháng 7 2021
Lời giải:
$(a+2b-c)(a+2b+c)-(a^2+4b^2-c^2)=(a+2b)^2-c^2-a^2-4b^2+c^2$
$=(a+2b)^2-a^2-4b^2$
$=a^2+4ab+4b^2-a^2-4b^2=4ab$
NT
2
TG
10 tháng 8 2021
\(\dfrac{1}{a-2b}.\sqrt{b^2\left(a^2-4ab+4b^2\right)}=\dfrac{1}{a-2b}.b.\left|a-2b\right|=\dfrac{1}{a-2b}.b.\left(2b-a\right)=-b\)
10 tháng 8 2021
\(\dfrac{1}{a-2b}\cdot\sqrt{b^2\cdot\left(a^2-4ab+b^2\right)}\)
\(=\dfrac{1\cdot\left(a-2b\right)}{a-2b}\cdot b\)
=b
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
AH
Akai Haruma
Giáo viên
13 tháng 12 2023
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$
NT
2
24 tháng 10 2021
1: \(a^2-4b^2-2a-4b\)
\(=\left(a-2b\right)\left(a+2b\right)-2\left(a+2b\right)\)
\(=\left(a+2b\right)\left(a-2b-2\right)\)
2: \(x^3+2x^2-2x-1\)
\(=\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+3x+1\right)\)
CM
30 tháng 10 2019
Ta có a 2 + 4 b 2 = 12 a b ⇔ a + 2 b 2 = 16 a b
Suy ra
2 log 3 a + 2 b = log 3 2 4 + log 3 a + log 3 b ⇔ log 3 a + 2 b = 2 log 3 2 + 1 2 log 3 a + log 3 b
Do đó cả hai mệnh đề đều sai
Đáp án C
14 tháng 8 2023
1: 2a+2b=2(a+b)
2: 2a+4b+6c
=2*a+2*2b+2*3c
=2(a+2b+3c)
3: \(-7a-14ab-21b=-7\left(a+2ab+3b\right)\)
4: \(2ax-2ay+2a=2a\left(x-y+1\right)\)
5: \(=3a\cdot ax-3a\cdot2ay+3a\cdot4=3a\left(ax-2ay+4\right)\)
6: \(=2\cdot2ax-2\cdot ay-2\cdot1=2\cdot\left(2ax-ay-1\right)\)
7: =a^2-(2b)^2
=(a-2b)(a+2b)
8: =(5a)^2-1^2
=(5a-1)(5a+1)
9: =9(16a^2-9)
=9(4a-3)(4a+3)
PA
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 2 2022
Đặt \(P=a+b+c\)
\(P^2=\left(a+b+c\right)^2=\left(1.a+\dfrac{1}{2}.2b+\dfrac{1}{3}.3c\right)^2\le\left(1^2+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2\right)\left(a^2+4b^2+9c^2\right)\)
\(\Rightarrow P^2\le\dfrac{49}{36}\left(a^2+4b^2+9c^2\right)=\dfrac{49}{36}\)
\(\Rightarrow-\dfrac{7}{6}\le P\le\dfrac{7}{6}\)
\(P_{min}=-\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(-\dfrac{6}{7};-\dfrac{3}{14};-\dfrac{2}{21}\right)\)
\(P_{max}=\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(\dfrac{6}{7};\dfrac{3}{14};\dfrac{2}{21}\right)\)
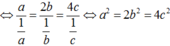
Ta có P=a^2+4b^2=(a^2-4ab+4b^2) +4ab
=(a-2b)^2+4ab=5^2+4*4=41
Vậy P=41 tại a-2b=5, ab=4
Ta có: (a-2b)^2 +4ab = 5^2 + 4.4
a^2 -4ab + 4b^2 +4ab = 25+16
a^2 + 4b^2 = 41
Vậy P =41