giải bất phương trình sau:
\(x^4-4x^2+8x-4>0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 12 2021
anh ơi, vậy là sai đề hả anh, chứ đề kêu chứng minh phương trình vô nghiệm mà em thấy anh ghi x=2
T
0
1
12 tháng 3 2020
x⁴ - 4x² + 12x - 9 = 0
<=> x⁴ - x³ + x³ - x² - 3x² + 3x + 9x - 9 = 0
<=> x³(x - 1) + x²(x - 1) - 3x(x - 1) + 9(x - 1) = 0
<=> (x - 1)(x³ + x² - 3x + 9) = 0
<=> (x - 1)(x³ + 3x² - 2x² - 6x + 3x + 9) = 0
<=> (x - 1)[ x²(x + 3) - 2x(x + 3) + 3(x + 3) ] = 0
<=> (x - 1)(x + 3)(x² - 2x + 3) = 0
<=> (x - 1)(x + 3)(x² - 2x + 1 + 2) = 0
<=> (x - 1)(x + 3)[ (x - 1)² + 2 ] = 0
<=> (x - 1)(x + 3) = 0 --> do (x - 1)² + 2 > 0 với mọi x
<=>
[ x - 1 = 0 =>[ x = 1
[ x + 3 = 0 =>[ x = -3
Bạn nên sửa >= là = vì giải bất phương trình mà
6 tháng 2 2021
\(4x^2-4x-5\left|2x-1\right|-5=0\)
\(\Leftrightarrow-5\left|2x-1\right|=5-4x^2+4x\)
\(\Leftrightarrow\left|2x-1\right|=\frac{-4x^2+4x+5}{-5}\)
\(\Leftrightarrow\left|2x-1\right|=\frac{4x\left(x-1\right)}{5}-1\)
TH1 : \(2x-1=\frac{4x\left(x-1\right)}{5}-1\Leftrightarrow2x=\frac{4x\left(x-1\right)}{5}\)
\(\Leftrightarrow10x=4x^2-4x\Leftrightarrow14x-4x^2=0\)
\(\Leftrightarrow-2x\left(2x-7\right)=0\Leftrightarrow x=0;x=\frac{7}{2}\)
TH2 : \(2x-1=-\left(\frac{4x\left(x-1\right)}{5}-1\right)\Leftrightarrow2x-1=-\frac{4x\left(x-2\right)}{5}+1\)
\(\Leftrightarrow2x-2=-\frac{4x\left(x-2\right)}{5}\Leftrightarrow10x-10=-4x^2+8x\)
\(\Leftrightarrow2x-10+4x^2=0\Leftrightarrow2\left(2x^2+x-5\ne0\right)=0\)tự chứng minh
Vậy tập nghiệm của phương trình là S = { 0 ; 7/2 }
N
5 tháng 6 2017
Vì x2 + 12 > 0 với mọi x
=> (4x-1)(x2+12)(-x+4) > 0
Khi ( (4x-1)(-x+4) > 0
TH1 : \(\hept{\begin{cases}4x-1>0\\-x+4>0\end{cases}}\)
<=> \(\hept{\begin{cases}x>\frac{1}{4}\\x< 4\end{cases}}\)
=> 1/4 < x < 4
TH2 \(\hept{\begin{cases}4x-1< 0\\-x+4< 0\end{cases}}\)
<=> \(\hept{\begin{cases}x< \frac{1}{4}\\x>4\end{cases}}\)
Vì không tồn tai x lớn hơn 4 và nhỏ hơn 1/4
=> TH2 không tồn tại x
=> (4x-1)(x2+12)(-x+4) > 0
khi 1/4 < x < 4
5 tháng 6 2017
Vì x^2 + 12 > 0 với mọi x
Ta có bất phương trình tương đương: (4x-1)(-x+4) > 0
=> 4x-1 và -x+4 phải cùng dấu.
Trường hợp 1: 4x-1 > 0 và -x + 4 > 0 <=> x>1/4 và x<4 <=> 1/4 < x < 4.
Trường hợp 2: 4x-1 < 0 và -x + 4 < 0 <=> x<1/4 và x>4 (vô lý)
Vậy S={x | 1/4 < x < 4}
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
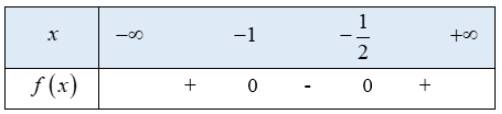
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:
Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
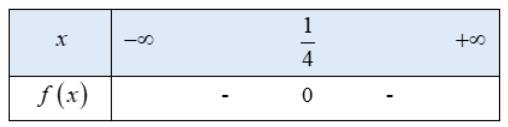
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
LS
0
16 tháng 5 2023
2:
a: =>2x^2-4x-2=x^2-x-2
=>x^2-3x=0
=>x=0(loại) hoặc x=3
b: =>(x+1)(x+4)<0
=>-4<x<-1
d: =>x^2-2x-7=-x^2+6x-4
=>2x^2-8x-3=0
=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)
ta có : \(x^4-4x^2+8x-4>0\Leftrightarrow\left(x^2-2x+2\right)\left(x^2+2x-2\right)>0\)
do \(x^2-2x+2>0\forall x\) rồi nên dấu của biểu thức phụ thuộc vào \(x^2+2x-2\) \(\Rightarrow\) bpt \(\Leftrightarrow x^2+2x-2>0\)
ta có : phương trình \(x^2+2x-2\) có 2 nghiệm \(\left[{}\begin{matrix}x=-1+\sqrt{3}\\x=-1-\sqrt{3}\end{matrix}\right.\)
và \(a=1>0\) \(\Rightarrow\) để \(x^2+2x-2>0\) thì \(\left[{}\begin{matrix}x>-1+\sqrt{3}\\x< -1-\sqrt{3}\end{matrix}\right.\)
vậy \(S=\left(-\infty;-1-\sqrt{3}\right)\cup\left(-1+\sqrt{3};+\infty\right)\)