tìm m để hàm số y=m2x4 - 2(4m-1)x2+1 đồng biến trên khoảng (1;+∞)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
+ Với ![]() , hàm số trở thành
, hàm số trở thành ![]() đồng biến trên
đồng biến trên ![]() nên hàm số cũng đồng biến trên khoảng
nên hàm số cũng đồng biến trên khoảng ![]() , do đó
, do đó ![]() thỏa mãn.
thỏa mãn.
+ Với ![]() , hàm số đã cho làm hàm số trùng phương với hệ số
, hàm số đã cho làm hàm số trùng phương với hệ số ![]() .
.
![]()
![]() ,
,
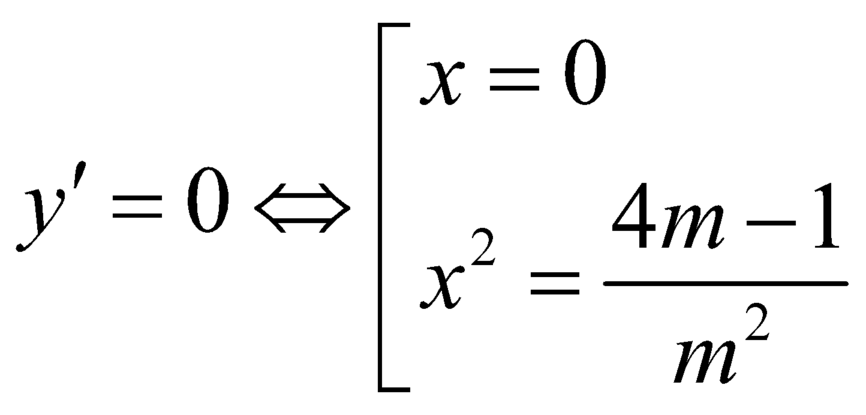 .
.
Để hàm số đồng biến trên khoảng ![]() thì phương trình
thì phương trình 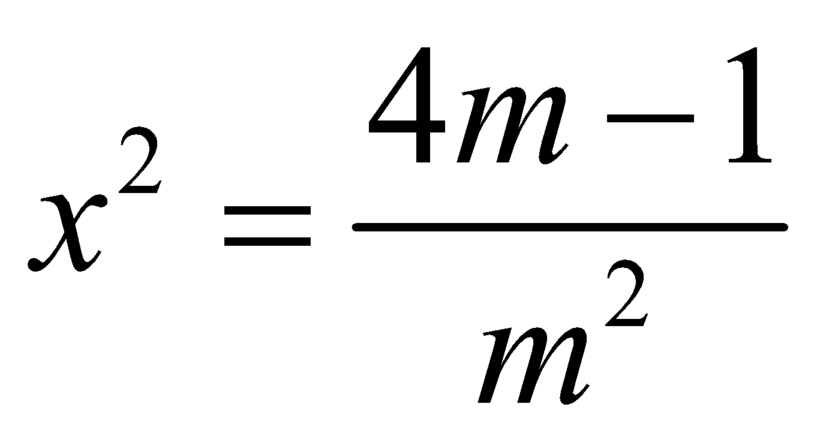 vô nghiệm hoặc có hai nghiệm phân biệt
vô nghiệm hoặc có hai nghiệm phân biệt ![]() ,
, ![]() sao cho
sao cho ![]()
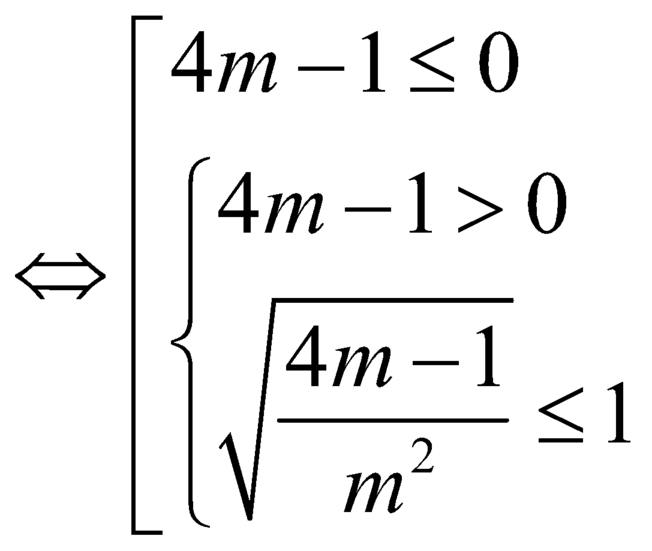
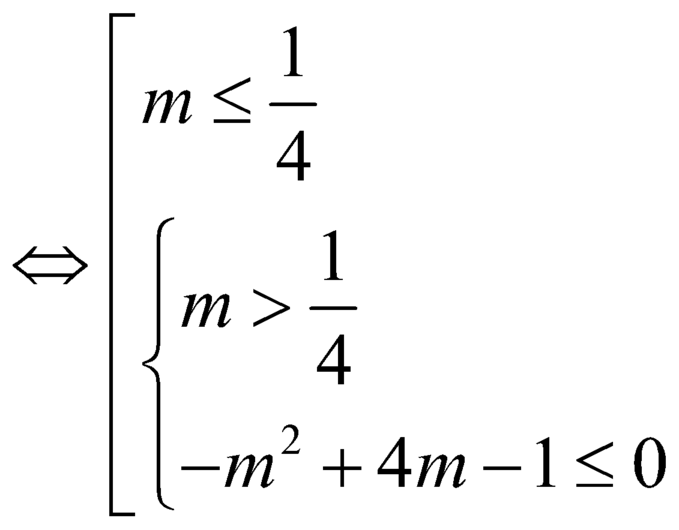
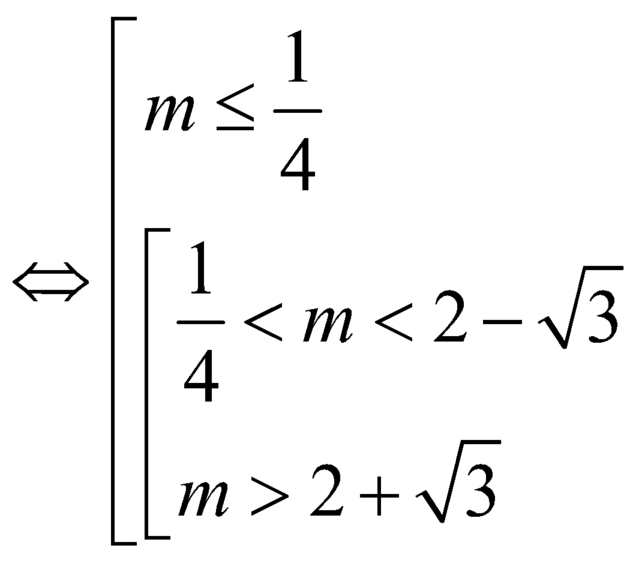 .
.
Vậy điều kiện để hàm số đồng biến trên ![]() là
là ![]() .
.
Vì ![]() nguyên,
nguyên, ![]() nên
nên ![]() , có
, có ![]() giá trị.
giá trị.

- Với \(m=0\) thỏa mãn
- Với \(-2\left(4m-1\right)\ge0\Rightarrow m\le\dfrac{1}{4}\) hàm đồng biến trên \(\left(0;+\infty\right)\) thỏa mãn
- Xét với \(m>\dfrac{1}{4}\)
\(y'=4m^2x^3-4x\left(4m-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\sqrt{4m-1}}{m}\\x=-\dfrac{\sqrt{4m-1}}{m}\end{matrix}\right.\)
Do \(a=m^2>0\) nên hàm đồng biến trên các khoảng \(\left(-\dfrac{\sqrt{4m-1}}{m};0\right)\) và \(\left(\dfrac{\sqrt{4m-1}}{m};+\infty\right)\)
\(\Rightarrow\) Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(\dfrac{\sqrt{4m-1}}{m}\ge1\Rightarrow4m-1\ge m^2\)
\(\Leftrightarrow m^2-4m+1\le0\Rightarrow2-\sqrt{3}\le m\le2+\sqrt{3}\)
Vậy \(\left[{}\begin{matrix}m\le\dfrac{1}{4}\\2-\sqrt{3}\le m\le2+\sqrt{3}\end{matrix}\right.\)

Chọn đáp án C.
Yêu cầu bài toán tương đương với
![]()
![]()
![]()
![]()
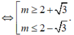
Vậy m ∈ - 9 , . . . , 0 , 4 , . . . , 9 có tất cả 16 số nguyên thoả mãn.

Đáp án C.
Ta có y ' = 4 m 2 x 3 − 4 4 m − 1 x
= 4 x m 2 x 2 − 4 m + 1 .
YCBT ⇔ y ' ≥ 0 , ∀ x ∈ 1 ; + ∞
⇔ m 2 x 2 − 4 m + 1 ≥ 0 , ∀ x ∈ 1 ; + ∞ (1)
Rõ ràng m = 0 thỏa mãn (1).
Với m ≠ 0 thì (1)
⇔ x 2 ≥ 4 m − 1 m 2 , ∀ x ∈ 1 ; + ∞ ⇔ 4 m − 1 m 2 ≤ 1 ⇔ m ≠ 0 m 2 − 4 m + 1 ≥ 0 ⇔ m ≠ 0 m ≥ 2 3 m ≤ 2 − 3 .
Kết hợp với m ∈ − 10 ; 10 m ∈ ℤ
⇒ m ∈ 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; − 9 ; − 8 ; − 7 ; − 6 ; − 5 ; − 4 ; − 3 ; − 2 ; − 1 .

Đáp án A
TXĐ: D= ℝ
y = m x 3 - x 2 + 2 x + m - 1
⇒ y ' = 3 m x 2 - 2 x + 2
Để y = m x 3 - x 2 + 2 x + m - 1 đồn biến trên khoảng - 2 ; 0 thì
y ' = 3 m x 2 - 2 x + 2 > 0 ∀ x ∈ - 2 ; 0
hay 2 x - 2 3 x 2 < m ∀ x ∈ - 2 ; 0
xét f x = 2 x - 2 3 x 2 có
f ' x = 2 . 3 x 2 - 6 x 2 x - 2 9 x 4 = - 6 x 2 + 12 x 9 x 4 = 0
⇔ x=0 hoặc x=2
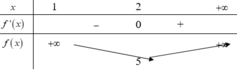
Ta có bảng biến thiên
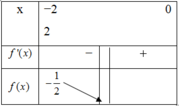
vậy f x = 2 x - 2 3 x 2 < m ∀ x ∈ - 2 ; 0 ⇔ m > - 1 2
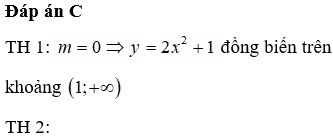




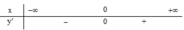





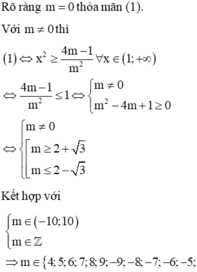

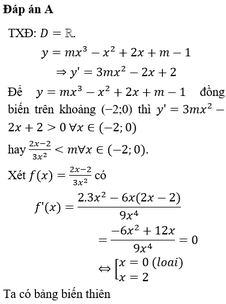



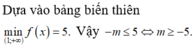
Lời giải:
Đặt \(x^2=t\). Khi đó: \(y=m^2t^2-2(4m-1)t+1\)
\(\Rightarrow y'=2m^2t-2(4m-1)\)
Hàm số ban đầu đồng biến trên \((1;+\infty)\) khi :
\(2m^2t-2(4m-1)\geq 0(*), \forall t\in (1;+\infty)\)
Với \(m=0\Rightarrow (*)\) luôn đúng (thỏa mãn)
Với \(m\geq 0; (*)\Leftrightarrow t\geq \frac{4m-1}{m^2}\) với mọi \(t\in (1;+\infty)\)
\(\Rightarrow \frac{4m-1}{m^2}\leq \min t\Rightarrow \frac{4m-1}{m^2}\leq 1\)
\(\Rightarrow 4m-1\leq m^2\Rightarrow \left[\begin{matrix} m\leq 2-\sqrt{3}\\ m\geq 2+\sqrt{3}\end{matrix}\right.\)
Vậy \(m\in (-\infty; 2-\sqrt{3}]; m\in [2+\sqrt{3}; +\infty)\)