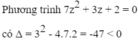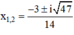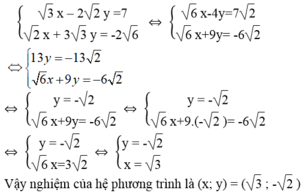Giải phương trình trên tập hợp N* : 3x5-19(72x-y)2=240677
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
5 tháng 1 2017
\(72x-\sqrt{\frac{3x^{^5}-240677}{19}}hay72x+\sqrt{\frac{3x^{^5}-240677}{19}}\). Suy ra: \(x\ge10\). Ghi vào màn hình:
\(A=A+1:B=72A-\sqrt{\frac{3A^{^5}-240677}{19}}:C=72A+\sqrt{\frac{3X^{^5}-240677}{19}}\). Cho A=9, rồi chạy để tìm kết quả.
QT
0
NT
1
ML
2 tháng 8 2016
\(pt\Leftrightarrow\left[\left(x-4\right)\left(x-10\right)\right]\left[\left(x-5\right)\left(x-8\right)\right]=72x^2\)
\(\Leftrightarrow\left(x^2+40-14x\right)\left(x^2+40-13x\right)=72x^2\)
\(x=0\) không phải là nghiệm của phương trình trên
Xét \(x\ne0\)
\(pt\Leftrightarrow\frac{x^2+40-14x}{x}.\frac{x^2+40-13x}{x}=72\)
\(\Leftrightarrow\left(x+\frac{40}{x}-14\right)\left(x+\frac{40}{x}-13\right)=72\)
Đặt \(x+\frac{40}{x}-14=a\)
\(pt\rightarrow a\left(a+1\right)=72\Leftrightarrow a^2+a-72=0\Leftrightarrow\orbr{\begin{cases}a=8\\a=-9\end{cases}}\)
TH1: a = 8 \(\Rightarrow x+\frac{40}{x}-14=8\Leftrightarrow\frac{x^2-22x+40}{x}=0\Leftrightarrow\orbr{\begin{cases}x=2\\x=20\end{cases}}\)
TH2: a = -9 \(\Rightarrow x+\frac{40}{x}-14=-9\Leftrightarrow\frac{x^2-5x+40}{x}=0\text{ }\left(\text{vô nghiệm }\right)\)
KN
1
19 tháng 1 2021
Bài này có trong báo THTT và đang trong thời hạn giải nên mình nghĩ bạn không nên đăng hỏi.
Với lại bài này có số mũ thực nên không thể là bài lớp 9.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2021
Với lớp 12 thì đây là 1 bài toán rất dễ
Nhưng lớp 9 thì nan giải :D
PT
1
