Chứng minh rằng nếu a + b = 1 thì a^2 + b^2 ≥ 1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
1
PT
1
2 tháng 9 2016
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac.
(1/a + 1/b + 1/c)² = 1/a² + 1/b² + 1/c² + 2(1/ab + 1/bc + 1/ac) = 4
<=> 1/a² + 1/b² + 1/c² + 2(bcac + abac + abbc)/(a²b²c²) = 4
<=> 1/a² + 1/b² + 1/c² + 2abc(a + b + c)/(a²b²c²) = 4
<=> 1/a² + 1/b² + 1/c² + 2 = 4
(vi` abc(a + b + c) = a² b² c²)
<=> 1/a² + 1/b² + 1/c² = 2 !!
24 tháng 5 2019
Áp dụng bđt Bunhiakovxki
\(\left(1^2+1^2\right)\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge1\)
\(\Leftrightarrow a^2+b^2\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=\frac{1}{2}\)
24 tháng 5 2019
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
NQ
1
18 tháng 9 2019
Ta có a + b =1 \(\Leftrightarrow b=1-a\)
Thay vào bất đẳng thức \(a^2+b^2\ge\frac{1}{2}\) , ta được:
\(a^2+\left(1-a\right)^2\ge\frac{1}{2}\Leftrightarrow a^2+1-2a+a^2̸̸\ge\frac{1}{2}\)
\(\Leftrightarrow2a^2-2a+1\ge\frac{1}{2}\Leftrightarrow4a^2-4a+2\ge1\)
\(\Leftrightarrow4a^2-4a+1\ge0\Leftrightarrow\left(2a-1\right)^2\ge0\) ( luôn đúng )
Vậy bất đẳng thức được chứng minh
Chúc bạn học tốt !!!
H
0
MN
Chứng minh rằng nếu a^2=bc thì a^2+c^2/b^2+a^2=c/b
Chứng minh rằng nếu a^2=bc thì a^2+c^2/b^2+a^2=c/b
2
27 tháng 12 2016
ta có: \(\frac{a^2+c^2}{b^2+a^2}\)do \(a^2=bc\)
=>\(\frac{a^2+c^2}{b^2+a^2}=\frac{b.c+c.c}{b.b+b.c}=\frac{c.\left(b+c\right)}{b.\left(b+c\right)}=\frac{c}{b}\)
vậy \(\frac{a^2+c^2}{b^2+a^2}=\frac{c}{b}\)
14 tháng 7 2021
\(\text{Ta có : }\frac{a^2+c^2}{b^2+a^2}\text{ do }a^2=bc\)
\(\Rightarrow\frac{a^2+c^2}{b^2+a^2}=\frac{b.c+c.c}{b.b+b.c}=\frac{c.\left(b+c\right)}{b.\left(b+c\right)}=\frac{c}{b}\)
\(\text{Vậy }\frac{a^2+c^2}{b^2+a^2}=\frac{c}{b}\)
TV
8
2 tháng 5 2016
Với mọi a, b ta có :
( a - b) 2 >= 0
<=> a2 - 2ab + b2 >= 0
<=> a2 + b2 >=2ab
<=> 2 ( a2 + b2 ) >= a2 +2ab + b2
<=> 2 (a2 + b2 ) >= ( a + b )2 mà a+b=1 nên 2 ( a2 + b2 ) >=1
<=> a2 + b2 >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
VN
2 tháng 5 2016
Với mọi a, b ta có :
( a - b) 2 >= 0
<=> a2 - 2ab + b2 >= 0
<=> a2 + b2 >=2ab
<=> 2 ( a2 + b2 ) >= a2 +2ab + b2
<=> 2 (a2 + b2 ) >= ( a + b )2 mà a+b=1 nên 2 ( a2 + b2 ) >=1
<=> a2 + b2 >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
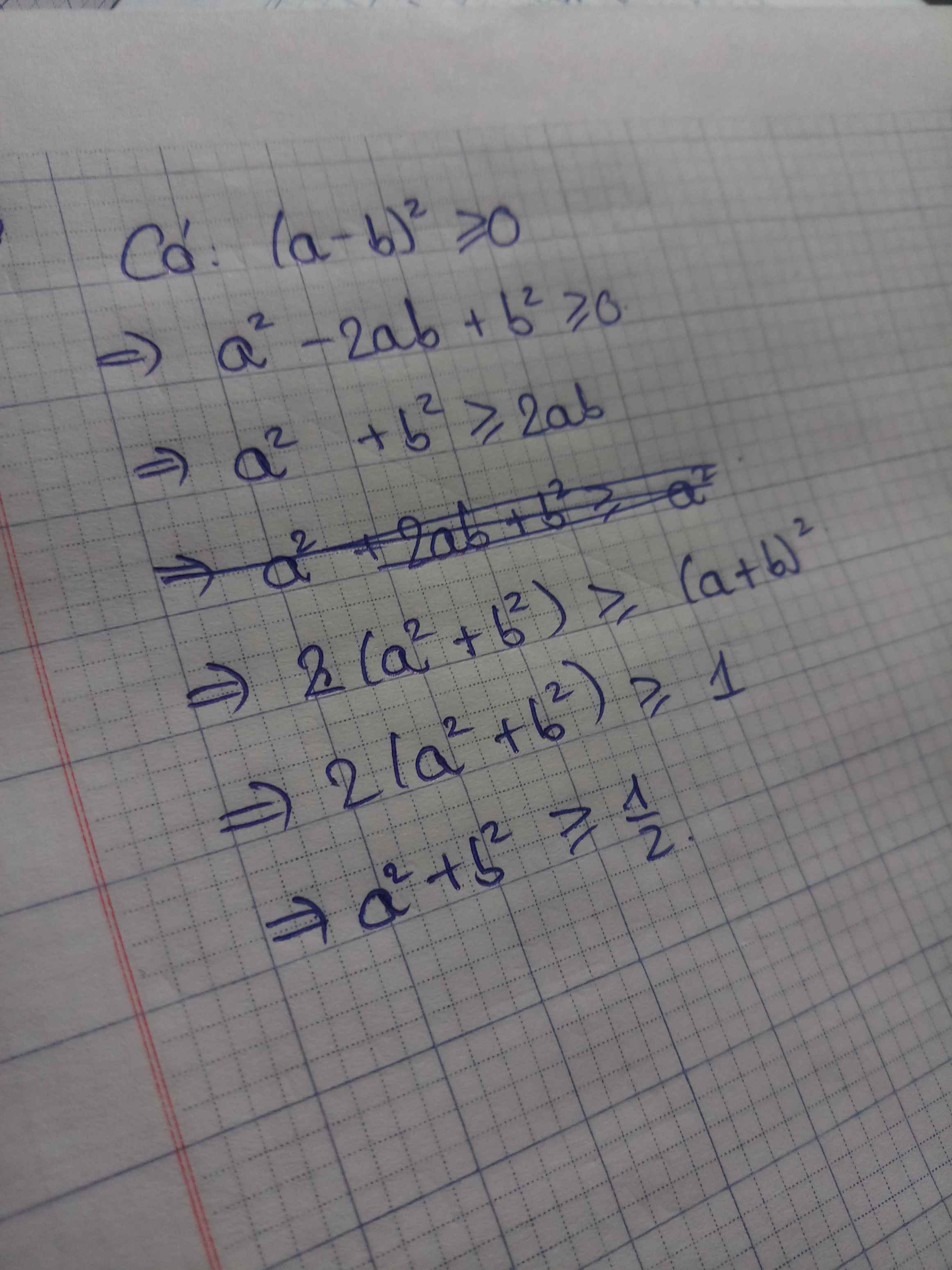
Giải:
Ta có: \(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow a^2+b^2+a^2+b^2\ge2ab+a^2+b^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge1^2=1\)
\(\Leftrightarrow a^2+b^2\ge\dfrac{1}{2}\left(đpcm\right)\)
Vậy ...
Cách khác :
Áp dụng BĐT Bunhiacopxki vào bài toán , ta có :
( a2 + b2)( 12 + 12) ≥ ( a + b)2
⇒ a2 + b2 ≥ \(\dfrac{\left(a+b\right)^2}{2}=\dfrac{1}{2}\)
Đẳng thức xảy ra khi và chỉ khi : a = b = \(\dfrac{1}{2}\)