Cho hình thang ABCD có hai đáy là AB và CD. Biết AB = 15 cm , CD = 20 cm;
chiều cao hình thang là 14cm. Hai đường chéo AC và BD cắt nhau ở E .
a) Tính diện tích hình thang ABCD.
b) Tính diện tích tam giác CED.
c) Chứng minh hai tam giác AED và BEC có diện tích bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E 20 15 14
+) Ta có: S(AED) = S(ADB) - S(AEB)
S(BEC) = S(ACB) - S(AEB)
mà S(ADB) = S(ACB) do chều cao hạ từ D và C xuống AB bằng nhau và chung đáy AB
=> S(AED) = S(BEC)
+) Ta có: S(ABC) = 14 x 15 : 2 = 105 cm2
S(ADC) = 14 x 20 : 2 = 140 cm2
=> S(ABC) / S(ACD) = 105 / 140 = 3/4
Tam giác ABC và ACD có chung đáy là AC nên
Chiều cao hạ từ B xuống AC / chiều cao hạ từ D xuống AC = 3/4
Mà tam giác BEC và AED có diện tích bằng nhau
=> đáy EC/ đáy AE = 3/4
+) Tam giác CED và tam giác AED có chùng chiều cao hạ từ D xuống AC
đáy EC/ AE = 3/4
=> S(CED)/ S(AED) = 3/4
=> S(CED)/ S(ACD) = 3/7 =>S (CED) = 3/7 x S(ACD) = 3/7 x 140 = 60 cm2
b) kẻ HK qua E vuông góc với 2 đáy.EK la chiều cao tg CDE.
Theo ĐL ta-let :
AB/CD=EH/EK
=>EK/HK=CD/(AB+CD) => EK=8cm
S = 80(cm2)

Hình bn tự vẽ nhá!
a, diện tích hình thang ABCD là: \(\frac{\left(15+20\right).14}{2}=245\left(cm^2\right)\)
b,\(\frac{BE}{DE}=\frac{S_{AEB}}{S_{AED}}=\frac{S_{CEB}}{S_{CED}}=\frac{S_{AEB}+S_{CEB}}{S_{AED}+S_{CED}}=\frac{S_{ABC}}{S_{ACD}}=\frac{AB}{CD}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{CEB}}{S_{CED}}=\frac{3}{4}\Rightarrow\frac{S_{CEB}+S_{CED}}{S_{CED}}=\frac{7}{4}\Rightarrow\frac{S_{DBC}}{S_{CED}}=\frac{7}{4}\)
\(\Rightarrow S_{CED}=\frac{4}{7}.S_{DBC}\)
\(S_{DBC}=\frac{20.14}{2}=140\left(cm^2\right)\)
\(\Rightarrow S_{CED}=\frac{4}{7}.140=80\left(cm^2\right)\)
c,\(S_{AED}=S_{ACD}-S_{ECD}\)
\(S_{BEC}=S_{BCD}-S_{ECD}\)
MÀ \(S_{ACD}=S_{BCD}\Rightarrow S_{AED}=S_{BEC}\)
Câu 5: Cho hình thang ABCD có đáy bé AB=1/3 đáy lớn.Chiều cao bằng 12,6m và bằng hiệu độ dài hai đáy. a,Tính diện tích hình thang ABCD. b,Hai đường chéo AC và BD cắt nhau tại O.So sánh diện tích hai tam giácOBC và OAD c, Kéo dài cạnh DA và CB cắt nhau tại P.Tính tỉ số hai tam giác DBP và DPC.

Qua A kẻ AE//BD (E Î DC)
Þ AE = BD = 12cm, DE = AB = 5cm
Þ DAEC vuông tại A (định lý Pytago đảo)
⇒ A H = A E . A C E C = 12.16 20 = 9 , 6 c m
Þ SABCD = 96cm2
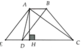

.Từ A và B kẻ AH,BK vuông góc với CD
AB+CD=40*
ABCD là ht cân=>DH=CK=>DK=AB+CK=20cm
=>▲ADH cân tại D
mà góc D =60* nên ▲ADH đều =>AH là đường cao đồng thời là đường trung tuyến =>DH=HK=KC=10cm=>CD=30cm

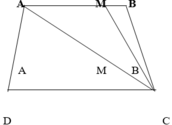
Đáy mới AM là: 15 – 5 = 10 (cm)
Tổng hai đáy AM và CD là : 10 + 20 = 30 (cm)
Chiều cao hình thang ABCD là : 280 x 2 : 5 = 112 (cm)
Diện tích hình thang ABCD là : 30 x 112 : 2 = 1680 (cm2)
Cách 2
Nối A với C
Ta có đoạn AM là : 15 – 5 = 10 (cm)
Diện tích tam giác ACM gấp 2 lần điện tích tam giác MCB Þ Diện tích tam giác ACM = 280 x 2 = 560 (cm2) (vì AM gấp BM hai lần và đường cao hai tam giác bằng nhau)
∆ DAC và ∆ MCB có :
DC gấp MB là
20 : 5 = 4 ( lần)
Đường cao chung nên diện tích tam giác DAC gấp diện tích tam giác
MCB 4 lần.
Diện tích tam giác ADC là : 280 x 4 = 1120 (cm2)
mỗi cái S là diện tích
a, diện tích hình thang ABCD là: (15+20).142=245(cm2)(15+20).142=245(cm2)
b,BEDE=SAEBSAED=SCEBSCED=SAEB+SCEBSAED+SCED=SABCSACD=ABCD=34BEDE=SAEBSAED=SCEBSCED=SAEB+SCEBSAED+SCED=SABCSACD=ABCD=34
⇒SCEBSCED=34⇒SCEB+SCEDSCED=74⇒SDBCSCED=74⇒SCEBSCED=34⇒SCEB+SCEDSCED=74⇒SDBCSCED=74
⇒SCED=47.SDBC⇒SCED=47.SDBC
SDBC=20.142=140(cm2)SDBC=20.142=140(cm2)
⇒SCED=47.140=80(cm2)⇒SCED=47.140=80(cm2)
c,SAED=SACD−SECDSAED=SACD−SECD
SBEC=SBCD−SECDSBEC=SBCD−SECD
MÀ SACD=SBCD⇒SAED=SBEC