Giải bất phương trình: ax+4 > 2x+a ( x là ẩn )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 8 2019
Điều kiện xác định: a ≠ 0.
Ta có: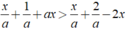
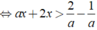
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là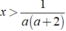
+ Nếu a < - 2 thì nghiệm của bất phương trình là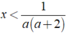
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
6 tháng 10 2023
Bất phương trình bậc nhất 2 ẩn :
\(2x+3y>0\Rightarrow Câu\) \(C\)
\(x-2y\le1\Rightarrow Câu\) \(f\)
\(4\left(x-1\right)+5\left(y-3\right)>2x-9\)
\(\Leftrightarrow4x-4+5y-15-2x+9>0\)
\(\Leftrightarrow2x+5y-10>0\) \(\Rightarrow Câu\) \(i\)
T
21 tháng 4 2018
1
a (9+x)=2 ta có (9+x)= 9+x khi 9+x >_0 hoặc >_ -9
(9+x)= -9-x khi 9+x <0 hoặc x <-9
1)pt 9+x=2 với x >_ -9
<=> x = 2-9
<=> x=-7 thỏa mãn điều kiện (TMDK)
2) pt -9-x=2 với x<-9
<=> -x=2+9
<=> -x=11
x= -11 TMDK
vậy pt có tập nghiệm S={-7;-9}
các cau con lai tu lam riêng nhung cau nhan với số âm thi phan điều kiện đổi chiều nha vd
nhu cau o trên mk lam 9+x>_0 hoặc x>_0
với số âm thi -2x>_0 hoặc x <_ 0 nha
ZT
1
18 tháng 6 2018
\(\Leftrightarrow m^2x+x< m-1\)
\(\Leftrightarrow\left(m^2+1\right)x< m-1\)
Vì \(m^2+1>0\)
\(m^2+1\ne0thi.x=\frac{m-1}{m^2+1}\)
\(m^2+1=0.thi.PT.vô.nghiệm\)
mình nghĩ vậy
CM
9 tháng 11 2019
- Bất phương trình a), c) là các bất phương trình bậc nhất một ẩn.
- Bất phương trình b) có a = 0 không thỏa mãn điều kiện a ≠ 0 nên không phải là bất phương trình bậc nhất một ẩn.
- Bất phương trình d) có mũ ở ẩn x là 2 nên không phải là bất phương trình bậc nhất một ẩn.
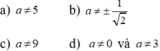
\(ax+4>2x+a\)
\(\Leftrightarrow ax-2x>a-4\)
\(\Leftrightarrow\left(a-2\right)x>a-4\)
Nếu \(a>2\) thì nghiệm của bất phương trình là \(x>\dfrac{a-4}{a-2}\)
Nếu \(a< 2\) thì nghiệm của bất phương trình là \(x< \dfrac{a-4}{a-2}\)
Nếu \(a=2\) thì bất phương trình có dạng \(0x>-2\), nghiệm đúng với mọi x
ax + 4 > 2x + a
<=> ax - 2x + a + 4 > 0
<=> x(a- 2) > - (a + 4)
<=> x > \(-\dfrac{a+4}{a-2}\) hoặc x < \(-\dfrac{a+4}{a-2}\)
(2 trường hợp vì ở đây a không có đk, nên có thể âm hoặc dương)