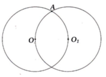
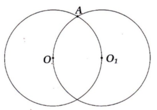
Cho hai đường tròn (O1; R1) và (O2; R2) với R1 > R2 tiếp xúc trong với nhau tại A. Đường thẳng O1O2 cắt (O1; R1) và (O2; R2) lần lượt tại B và C khác A. Đường thẳng đi qua trung điểm D của BC vuông góc với BC cắt (O1; R1) tại P và Q.
1) Chứng minh C là trực tâm tam giác APQ
2) Chứng minh DP2 = R12 - R22
3) Giả sử D1; D2; D3; D4 lần lượt là hình chiếu vuông góc của D xuống các đường thẳng BP;PA;AQ;QB. Chứng minh DD1 + DD2 + DD3 + DD4 ≤ \(\dfrac{1}{2}\)(BP + PA + AQ + QB)
(Giúp mình với, mình đang cần gấp)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.

a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .

a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c, P M H ^ = M B H ^ => P Q H ^ = O 2 Q B ^ => PQ là tiếp tuyến của O 2
Tương tự PQ cũng là tiếp tuyến ( O 1 )