Giúp em bài min này với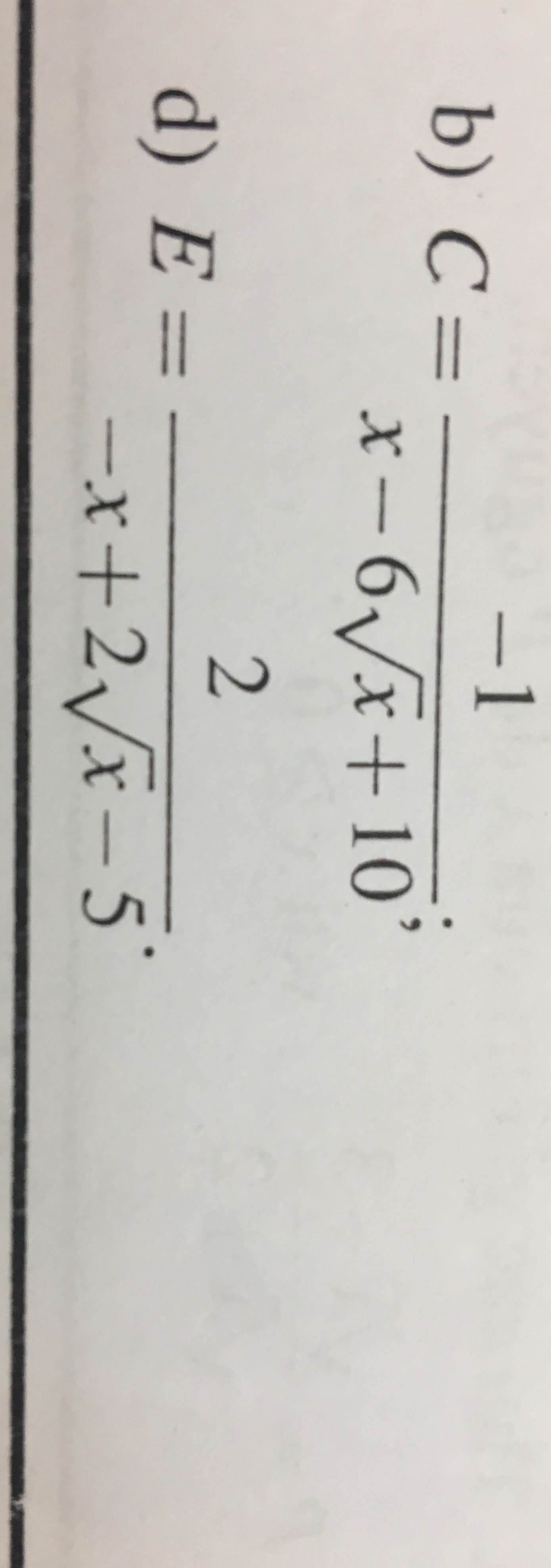 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 9 2021
\(B=\dfrac{2}{-1-\left(x-4\sqrt{x}+4\right)}=\dfrac{2}{-1-\left(\sqrt{x}-2\right)^2}\ge\dfrac{2}{-1}=-2\)
\(B_{min}=-2\) khi \(x=4\)
\(D=\dfrac{-3}{x+8\sqrt{x}+20}\ge-\dfrac{3}{20}\)
\(D_{min}=-\dfrac{3}{20}\) khi \(x=0\)
9 tháng 9 2021
\(A=\dfrac{2}{4\sqrt{x}-x-5}=\dfrac{2}{-\left(x-4\sqrt{x}+4+1\right)}=\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\)
\(-\left(\sqrt{x}-2\right)^2-1\le-1\\ \Leftrightarrow\dfrac{2}{-\left(\sqrt{x}-2\right)^2-1}\ge-2\)
Dấu \("="\Leftrightarrow x=4\)
\(B=\dfrac{-3}{x+8\sqrt{x}+20}=\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\)
\(\left(\sqrt{x}+4\right)^2+4\ge4\\ \Leftrightarrow\dfrac{3}{\left(\sqrt{x}+4\right)^2+4}\le\dfrac{3}{4}\\ \Leftrightarrow\dfrac{-3}{\left(\sqrt{x}+4\right)^2+4}\ge-\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\sqrt{x}+4=0\Leftrightarrow x\in\varnothing\)
Vậy dấu \("="\) không xảy ra
TH
0
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2023
\(2ab+6bc+2ac=7abc\Rightarrow\dfrac{6}{a}+\dfrac{2}{b}+\dfrac{2}{c}=7\)
Đặt \(\left(\dfrac{2}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow3x+2y+2z=7\)
\(C=\dfrac{4}{\dfrac{2}{a}+\dfrac{1}{b}}+\dfrac{9}{\dfrac{4}{a}+\dfrac{1}{c}}+\dfrac{4}{\dfrac{1}{b}+\dfrac{1}{c}}=\dfrac{4}{x+y}+\dfrac{9}{2x+z}+\dfrac{4}{y+z}\)
\(C\ge\dfrac{\left(2+3+2\right)^2}{x+y+2x+z+y+z}=\dfrac{49}{7}=7\)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(\left(a;b;c\right)=\left(2;1;1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
Đặt \(x=\sqrt{\dfrac{a}{bc}}\) ; \(y=\sqrt{\dfrac{b}{ca}}\) ; \(z=\sqrt{\dfrac{c}{ab}}\)
\(\Rightarrow a=\dfrac{1}{yz}\) ; \(b=\dfrac{1}{zx}\) ; \(c=\dfrac{1}{xy}\)
\(\Rightarrow xy+yz+zx=1\)
Khi đó, tồn tại một tam giác ABC sao cho:
\(x=tan\dfrac{A}{2}\) ; \(y=tan\dfrac{B}{2}\) ; \(z=tan\dfrac{C}{2}\)
Thay vào bài toán:
\(A=\dfrac{x^2}{1+x^2}+\sqrt{3}\left(\dfrac{y^2}{1+y^2}+\dfrac{z^2}{1+z^2}\right)\)
\(=\dfrac{tan^2\dfrac{A}{2}}{1+tan^2\dfrac{A}{2}}+\sqrt{3}\left(\dfrac{tan^2\dfrac{B}{2}}{1+tan^2\dfrac{B}{2}}+\dfrac{tan^2\dfrac{C}{2}}{1+tan^2\dfrac{C}{2}}\right)\)
\(=sin^2\dfrac{A}{2}+\sqrt{3}\left(sin^2\dfrac{B}{2}+sin^2\dfrac{C}{2}\right)\)
\(=\dfrac{1}{2}-\dfrac{1}{2}cosA+\dfrac{\sqrt{3}}{2}\left(2-cosB-cosC\right)\)
\(=\dfrac{1+2\sqrt{3}}{2}-\dfrac{1}{2}\left(cosA+\sqrt{3}cosB+\sqrt{3}cosC\right)\)
Xét \(B=cosA+\sqrt{3}\left(cosB+cosC\right)=cosA+2\sqrt{3}cos\dfrac{B+C}{2}cos\dfrac{B-C}{2}\)
\(\le cosA+2\sqrt{3}cos\dfrac{B+C}{2}=-2sin^2\dfrac{A}{2}+2\sqrt{3}sin\dfrac{A}{2}+1\)
Xét hàm \(f\left(t\right)=-2t^2+2\sqrt{3}sint+1\) với \(t\in\left(0;1\right)\)
\(f'\left(t\right)=-4t+2\sqrt{3}=0\Rightarrow t=\dfrac{\sqrt{3}}{2}\)
\(f\left(0\right)=1\) ; \(f\left(\dfrac{\sqrt{3}}{2}\right)=\dfrac{5}{2}\) ; \(f\left(1\right)=2\sqrt{3}-1\)
\(\Rightarrow B_{max}=\dfrac{5}{2}\)
\(\Rightarrow A\ge\dfrac{1+2\sqrt{3}}{2}-\dfrac{5}{4}=\dfrac{4\sqrt{3}-3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
Áp dụng BĐT Mincopxki:
\(P\ge\sqrt{\left(a+b+c\right)^2+2\left(a+b+c\right)^2}=\sqrt{3}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Lại có do \(a;b;c\ge0\) nên:
\(a^2+2b^2\le a^2+2\sqrt{2}ab+2b^2=\left(a+\sqrt{2}b\right)^2\)
\(\Rightarrow\sqrt{a^2+2b^2}\le a+\sqrt{2}b\)
Tương tự và cộng lại:
\(\Rightarrow P\le\left(\sqrt{2}+1\right)\left(a+b+c\right)=\sqrt{2}+1\)
Dấu "=" xảy ra tại \(\left(a;b;c\right)=\left(1;0;0\right)\) và các hoán vị
TD
0
NB
2
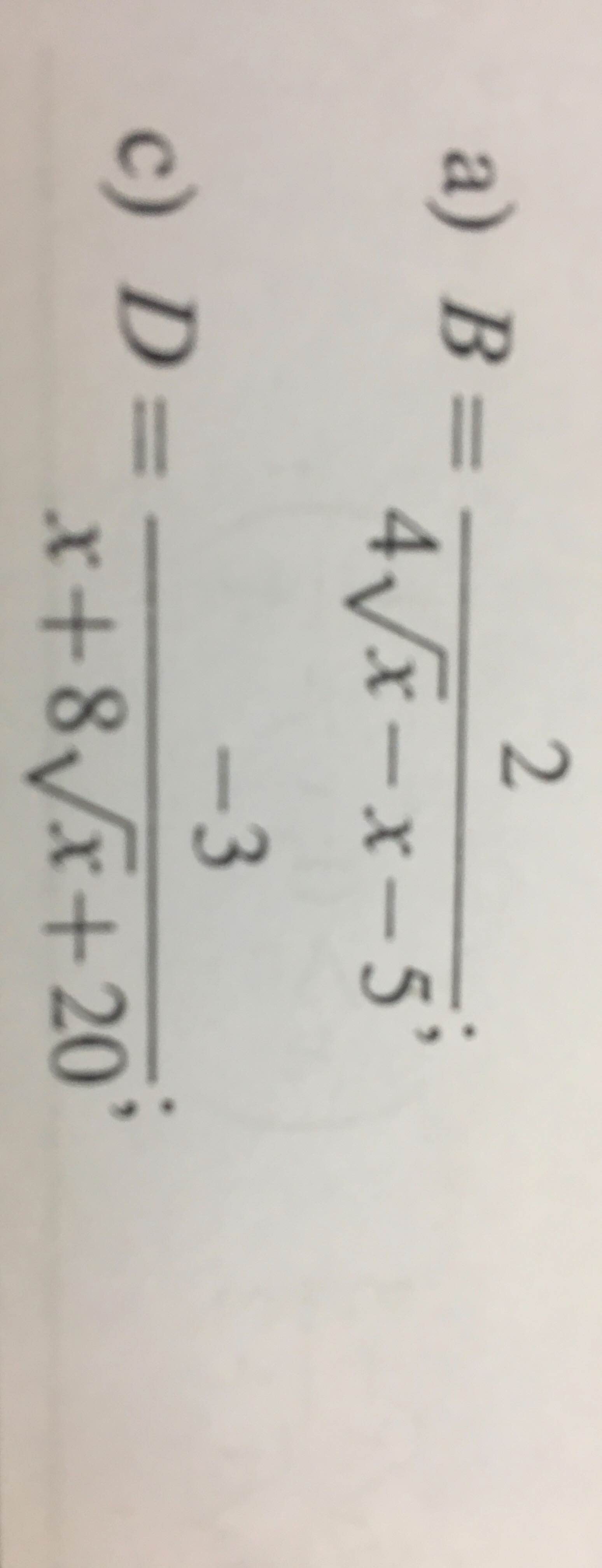
\(C=\dfrac{-1}{\left(x-6\sqrt{x}+9\right)+1}=\dfrac{-1}{\left(\sqrt{x}-3\right)^2+1}\ge\dfrac{-1}{1}=-1\)
\(C_{min}=-1\) khi \(x=9\)
\(E=\dfrac{2}{-4-\left(x-2\sqrt{x}+1\right)}=\dfrac{2}{-4-\left(\sqrt{x}-1\right)^2}\ge\dfrac{2}{-4}=-\dfrac{1}{2}\)
\(E_{min}=-\dfrac{1}{2}\) khi \(x=1\)