Chứng minh rằng các bất phương trình sau có nghiệm là mọi số thực x
2x2-2x+1>0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
23 tháng 11 2018
(1) Phương trình 1 có nghiệm
<=> \(\Delta'\ge0\)<=> \(1-m\ge0\Leftrightarrow m\le1\)
(2) Gọi x1 , x2 là 2 nghiệm của phương trình
x1+x2=2>0 => Phương trình có ít nhất một nghiệm dương => Không thẻ có 2 nghiệm cùng là số âm
(3) x1+x2=2, x1-2x2=5
=> x1=3, x2=-1
mà x1.x2=m => m=-3
CM
10 tháng 4 2019
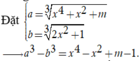
Khi đó bất phương trình trở thành
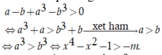
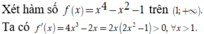
Suy ra hàm số f(x) đồng biến trên 
Do đó yêu cầu bài toán 
Chọn B.
TT
1
29 tháng 3 2017
\(A=x^2-x+1\)
\(A=\left(x^2-\dfrac{1}{2}.2.x+\dfrac{1}{4}\right)-\dfrac{1}{4}+1\)
\(A=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
\(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\in R\)
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\forall x\in R\)
Vậy: \(A>0\forall x\in R\) (đpcm)
2x2 - 2x + 1 > 0
⇔ x2 - x + \(\dfrac{1}{2}\) > 0
⇔ (x - \(\dfrac{1}{2}\) )2 + \(\dfrac{1}{4}\) > 0 luôn đúng.