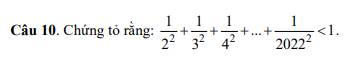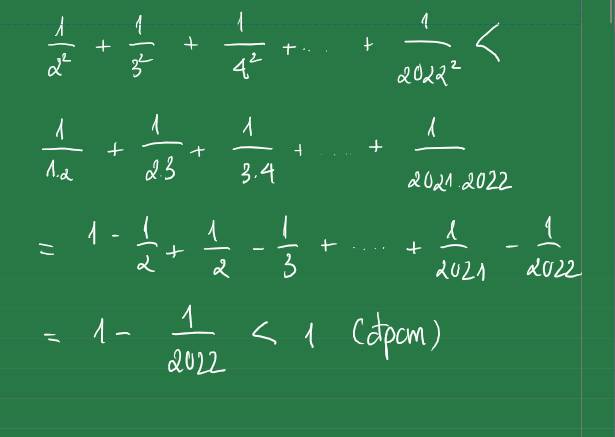Giúp em vs ạ, em cảm ơn rất nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
0
Những câu hỏi liên quan
KT
1
PL
30 tháng 8 2022
Bài 1: \(n_{CuO}=\dfrac{3,2}{80}=0,04\left(mol\right)\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
0,04 → 0,04
\(\Rightarrow m_{H_2SO_4}=0,04\cdot98=3,92\left(g\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{3,92}{80}\cdot100\%=4,9\%\)
Bài 2: \(n_{HCl}=0,2\cdot2=0,4\left(mol\right)\)
\(Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2\uparrow\)
\(\dfrac{1}{15}\) ← 0,4
\(\Rightarrow m_{Fe_2O_3}=\dfrac{1}{15}\cdot160=\dfrac{32}{3}\left(g\right)\)
16 tháng 1 2024
a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB
DT
1
5 tháng 11 2021
a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
=> BC là đường trung trực AD
\(\Rightarrow AD\perp BC\)
Áp dụng HTL trong tam giác BDC vuông tại D:
\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)
DT
1
13 tháng 11 2021
\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)
3T
0
NT
3
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
c/
$C=\frac{11}{2}(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{91.93})$
$=\frac{11}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+...+\frac{93-91}{91.93}\right)$
$=\frac{11}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+....+\frac{1}{91}-\frac{1}{93}\right)$
$=\frac{11}{2}(1-\frac{1}{93})$
$=\frac{11}{2}.\frac{92}{93}=\frac{506}{93}$
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
d/
$D=5\left(\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+...+\frac{1}{675}\right)$
$=\frac{5}{2}\left(\frac{2}{3}+\frac{2}{15}+\frac{2}{35}+...+\frac{2}{675}\right)$
$=\frac{5}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+...+\frac{27-25}{25.27}\right)$
$=\frac{5}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{25}-\frac{1}{27}\right)$
$=\frac{5}{2}\left(1-\frac{1}{27}\right)$
$=\frac{5}{2}.\frac{26}{27}=\frac{65}{27}$