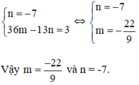Tìm đa thức P(x) bậc 5 sao cho P(x) +1 chia hết cho (x-1)3 và P(x) -1 chia hết cho (x+1)3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Nội suy đa thức, nhỉ?)
Để giải dạng bài này anh thường làm như sau:
Bước 1: Tìm coi \(P\left(x\right)\) có giả thiết gì rồi.
Qua các giả thiết đề cho ta biết được \(P\left(-2\right)=0\), \(P\left(1\right)=6\) và \(P\left(-1\right)=4\).
-----
Bước 2: Nội suy.
Viết \(P\left(x\right)\) dưới dạng \(a\left(x+2\right)+b\left(x+2\right)\left(x+1\right)+c\left(x+2\right)\left(x+1\right)\left(x-1\right)+d\).
Ta có \(P\left(-2\right)=d=0\).
Lại có \(P\left(-1\right)=a+d=4\Rightarrow a=4\)
Lại có \(P\left(1\right)=3a+6b+d=6\Rightarrow b=-1\).
Vậy đa thức \(P\left(x\right)=c\left(x+2\right)\left(x+1\right)\left(x-1\right)-\left(x+2\right)\left(x+1\right)+4\left(x+2\right)\) với \(c\) tuỳ ý

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
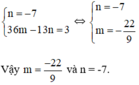

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :