GTNN của BT \(x^2-2x+y^2-4y+7\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CB
2
HT
1 tháng 9 2020
Đề đúng: \(C=x^2+4y^2+2x-4y-4xy+2011\)
\(C=\left(x^2-4xy+4y^2\right)+\left(2x-4y\right)+1+2010\)
\(C=\left(x-2y\right)^2+2\left(x-2y\right)+1+2010\)
\(C=\left(x-2y+1\right)^2+2010\ge2010\)
Dấu "=" xảy ra khi: \(\left(x-2y+1\right)^2=0\)
=> Ta có vô số cặp (x;y) thỏa mãn ví dụ như:
(1;1) ; (-1;0) ; (3;2) ; ...
1 tháng 9 2020
C = x2 + 4y2 + 2x - 4y - 4xy + 2011 ( đúng chưa :v )
C = [ ( x2 - 4xy + 4y2 ) + 2x - 4y + 1 ] + 2010
C = [ ( x - 2y )2 + 2( x - 2y ) + 1 ] + 2010
C = [ ( x - 2y ) + 1 ]2 + 2010
C = ( x - 2y + 1 )2 + 2010 ≥ 2010 ∀ x,y
Đẳng thức xảy ra <=> x - 2y + 1 = 0
<=> x - 2y = -1
<=> x = 2y - 1
=> MinC = 2011 <=> x = 2y - 1
NH
2
21 tháng 8 2016
Ta có:
A=x^2 - 2*3x + 9 +2(y^2 - 2y +1) + 7
=(x-3)^2 +2(y-1)^2 +7 >+ 7
=> minA= 7 <=> x=3 và y=1
PT
11 tháng 9 2018
a) \(A=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(A=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\)
\(A=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(A=\left(x^2+5x\right)^2-6^2\)
\(A=\left(x^2+5x\right)^2-36\)
Vì \(\left(x^2+5x\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x^2+5x\right)^2-36\ge-36\)
\(\Rightarrow Amin=-36\Leftrightarrow x^2+5x=0\)
\(\Rightarrow x\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
b) \(B=x^2-2x+y^2+4y+8\)
\(B=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+3\)
\(B=\left(x-1\right)^2+\left(y+2\right)^2+3\)
Vì \(\left(x-1\right)^2\ge0\) với mọi x
\(\left(y+2\right)^2\ge0\) với mọi y
\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\) với mọi x,y
\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2+3\ge3\)
\(\Rightarrow Bmin=3\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
c) \(C=x^2-4x+y^2-8y+6\)
\(C=\left(x^2-4x+4\right)+\left(y^2-8y+16\right)-14\)
\(C=\left(x-2\right)^2+\left(y-4\right)^2-14\)
Vì \(\left(x-2\right)^2\ge0\) với mọi x
\(\left(y-4\right)^2\ge0\) với mọi y
\(\Rightarrow\left(x-2\right)^2+\left(y-4\right)^2-14\ge-14\) với mọi x,y
\(\Rightarrow Cmin=-14\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\)
24 tháng 9 2021
\(H=x^2-2x+y^2-4y+7=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(minH=2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
18 tháng 6 2019
\(C=x^2+2x-y^2+4y-7\)
\(C=x^2+2x-y^2+4x+1-4-4\)
\(C=\left(x^2+2x+1\right)-\left(y^2-4y+4\right)-4\)
\(C=\left(x+1\right)^2-\left(y-2\right)^2-4\)
Vì \(\left(x+1\right)^2\ge0;\left(y-2\right)^2\ge0\)
\(\Rightarrow C=\left(x+1\right)^2-\left(y-2\right)^2-4\ge0-0-4\)
\(\Rightarrow C\ge-4\)
Vậy\(GTNN_C=-4\)tại \(x=-1\)và \(y=2\)
AH
Akai Haruma
Giáo viên
27 tháng 10 2018
1)
Ta có:
\(A=x^2+5y^2-2xy+4y+3=(x^2+y^2-2xy)+4y^2+4y+3\)
\(=(x^2-2xy+y^2)+(4y^2+4y+1)+2\)
\(=(x-y)^2+(2y+1)^2+2\)
Thấy rằng: \((x-y)^2\geq 0; (2y+1)^2\geq 0 , \forall x,y\)
\(\Rightarrow A\geq 0+0+2=2\)
Vậy GTNN của $A$ là $2$. Dấu "=" xảy ra khi \(\left\{\begin{matrix} (x-y)^2=0\\ (2y+1)^2=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=-\frac{1}{2}\\ y=\frac{1}{2}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
27 tháng 10 2018
2)
Đặt \(x^2-2x=a\)
Khi đó: \(B=a(a+2)=a^2+2a+1-1=(a+1)^2-1\)
\(=(x^2-2x+1)^2-1\)
\(=(x-1)^4-1\)
Thấy rằng \((x-1)^4\geq 0, \forall x\Rightarrow B\geq 0-1=-1\)
Vậy GTNN của $B$ là $-1$ khi \((x-1)^4=0\Leftrightarrow x=1\)
11 tháng 11 2017
A=x2+2xy+2y2-2x-4y+2
=x2+xy-x+y2+xy-y-x-y+1+y2-2y+1
=(x2+xy-x)+(y2+xy-y)-(x+y-1)+(y2-2y+1)
= x(x+y-1)+y(y+x-1)-(x+y-1)+(y-1)2
=(x+y-1)(x+y-1)+(y-1)2
A=(x+y-1)2+(y-1)2
do (x+y-1)2\(\ge0\forall x;y\)
(y-1)2\(\ge0\forall y\)
=>(x+y-1)2+(y-1)2\(\ge0\)
=>Min A=0 khi
x+y-1=0
=>x+y=1 (*)
y-1=0
=>y=1
thay y=1 vào (*) ta đc
x+1=1
=>x=0
vậy....
NN
11 tháng 11 2017
3) \(B=3x^2+x+7\)
\(\Leftrightarrow B=3x^2+x+\dfrac{1}{12}+\dfrac{83}{12}\)
\(\Leftrightarrow B=3\left(x^2+\dfrac{1}{3}x+\dfrac{1}{36}\right)+\dfrac{83}{12}\)
\(\Leftrightarrow B=3\left[x^2+2.x.\dfrac{1}{6}+\left(\dfrac{1}{6}\right)^2\right]+\dfrac{83}{12}\)
\(\Leftrightarrow B=3\left(x+\dfrac{1}{6}\right)^2+\dfrac{83}{12}\)
Vậy GTNN của \(B=\dfrac{83}{12}\) khi \(x+\dfrac{1}{6}=0\Leftrightarrow x=\dfrac{-1}{6}\)
HA
3
30 tháng 10 2017
2x2+4y2+4xy+2x+4y+9
=x2 +4y2+4xy+1+2x+4y+x2+9
=(x+2y)2+2(x+2y)+1+x2+9
=(x+2y+1)2+x2+9
có (x+2y+1)2≥0 với mọi x,y
x2≥0 với mọi x
⇒(x+2y+1)2+x2 ≥0với mọi x,y
⇒(x+2y+1)2+x2+9≥9với mọi x,y
⇒
30 tháng 10 2017
ta có :
A = 2x2+4y2+4xy+2x+4y+9 = 2x2+2x+4y2+4y+4xy+9
= 2x(x+1)+4y(y+1)+4xy+9
= 2x(x+1)+4y(y+x+1)+9
= (x+1)(2x+4y2)+9
=> A lớn hơn hoặc bằng 9
=> min A là 9
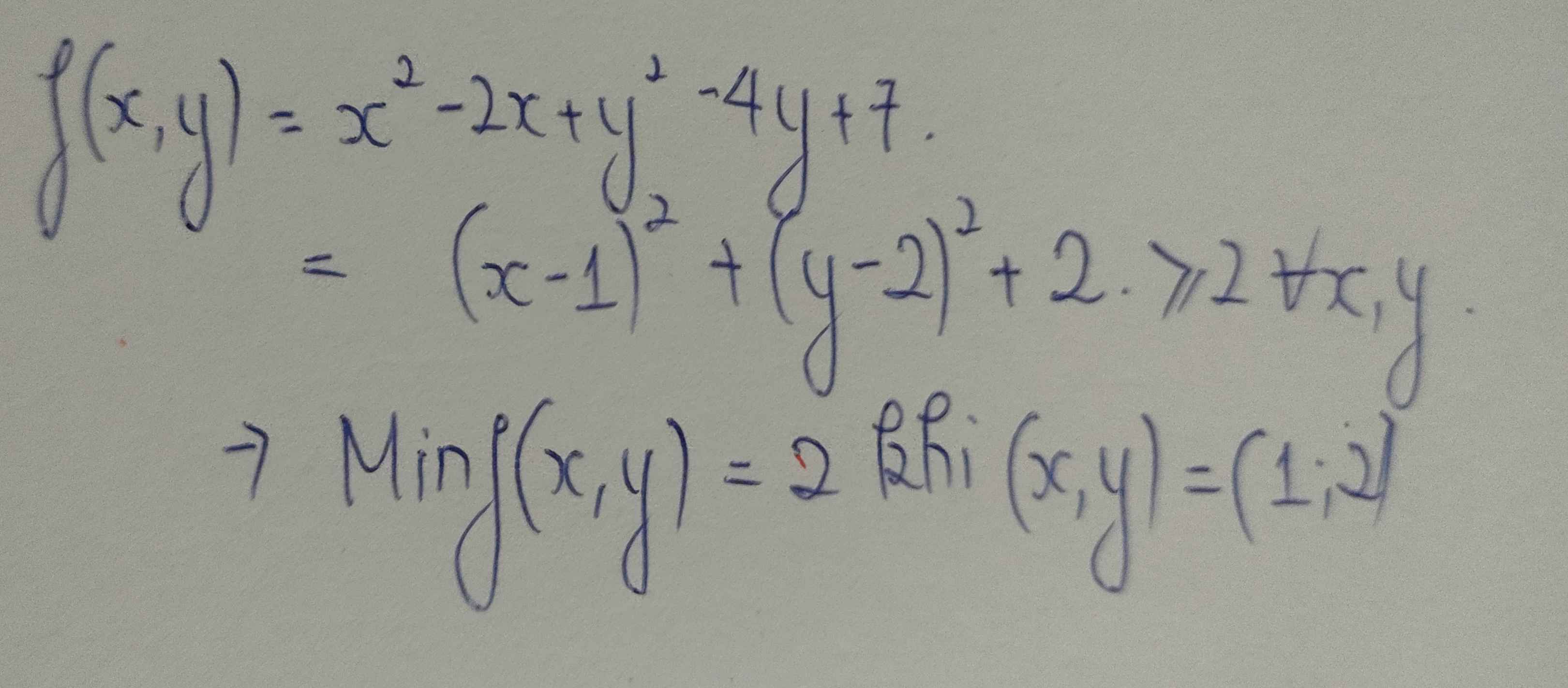
Lời giải:
Ta có: \(x^2-2x+y^2-4y+7\)
\(=(x^2-2x+1)+(y^2-4y+4)+2\)
\(=(x-1)^2+(y-2)^2+2\)
Ta thấy: \(\left\{\begin{matrix} (x-1)^2\geq 0\\ (y-2)^2\geq 0\end{matrix}\right.\forall x,y\in\mathbb{R}\)
Do đó: \((x-1)^2+(y-2)^2+2\geq 0+0+2\)
hay \(x^2-2x+y^2-4y+7\geq 2\)
Vậy GTNN của biểu thức là $2$
Dấu bằng xảy ra khi \(\left\{\begin{matrix} x-1=0\\ y-2=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=1\\ y=2\end{matrix}\right.\)