chứng minh
a^2+5b^2-(3a+b)>=3ab-5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ND
Nhã Doanh
20 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
TX
0
TT
1
25 tháng 3 2018
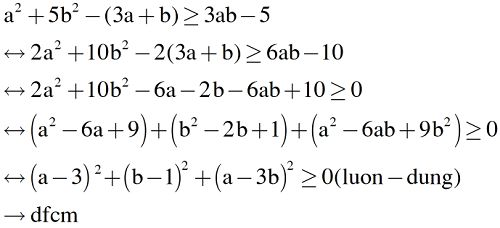
Links:
Chứng minh $a^2+5b^2-(3a+b)\geq 3ab-5$ - Bất đẳng thức và cực trị - Diễn đàn Toán học
Chứng minh a^2 + 5b^2 - (3a + b) ≥ 3ab - 5 - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
FT
1
TN
22 tháng 3 2017
\(a^2+5b-\left(3a+b\right)\ge3ab-5\)
\(\Leftrightarrow2a^2+10b^2-6a-2b-6ab+10\ge0\)
\(\Leftrightarrow\left(a^2-6ab+9b^2\right)+\left(a^2-6a+9\right)+\left(b^2-2b+1\right)\ge0\)
\(\Leftrightarrow\left(a-3b\right)^2+\left(a-3\right)^2+\left(b-1\right)^2\ge0\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}a-3b=0\\a-3=0\\b-1=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}a=3\\b=1\end{cases}}\)
Dễ thế này cũng hỏi nổi, LẠY @@
6 tháng 6 2015
10a^2 + 6ab- 5ab - 3b^2=0 <=>
<=> (2a-b)(3a+5b)=0 <=>2a = b hoặc 3a = -5b(loại vi b>a>0)
Thay 2a = b vào vế trái ta có
\(\frac{2a-2a}{3a-2a}+\frac{5.2a-a}{3a+2a}=0+\frac{9}{5}=\frac{9}{5}\)
Vậy vế trái bằng vế phải đẳng thức được chứng minh
TN
17 tháng 11 2016
Từ \(6a^2+ab=35b^2\)\(\Rightarrow6a^2+ab-35b^2=0\)
\(\Rightarrow6a^2+15ab-14ab-35b^2=0\)
\(\Rightarrow3a\left(2a+5b\right)-7b\left(2a+5b\right)=0\)
\(\Rightarrow\left(3a-7b\right)\left(2a+5b\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3a=7b\\2a=-5b\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}a=\frac{7b}{3}\\a=-\frac{5b}{2}\end{cases}}\)
Thay vao tinh....
30 tháng 4 2017
đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Thay a và c vào VP và VT sẽ bằng nhau
Ai help me vs
15 tháng 11 2016
Ta có : \(6a^2+ab=25b^2\)
Vì a,b > 0 nên chia cả hai vế cho a2 được : \(6+\frac{b}{a}=\frac{25b^2}{a^2}\)
Đặt \(t=\frac{b}{a}\) thì ta có \(25t^2-t-6=0\Leftrightarrow\orbr{\begin{cases}t=\frac{1+\sqrt{601}}{50}\\t=\frac{1-\sqrt{601}}{50}\end{cases}}\)
Tới đây bạn suy ra tỉ số giữa a và b rồi thay vào tính M nhé!
VK
9
2 tháng 5 2020
Bài làm
Ta có: 3a3 + 3a2b + 3ab2 + 3b3
= 3( a3 + a2b + ab2 + b3 )
= 3[ a2( a + b ) + b2( a + b ) ]
= 3( a2 + b2 )( a + b )
Ta có: ( a2 + b2 ) > 0 V a, b
=> ( a2 + b2 ) . 3 > 0
Mà 3( a2 + b )2( a + b ) > 0 ( đpcm )
2 tháng 5 2020
\(3a^3+3a^2b+3ab^2+3b^3>0\)
\(\Leftrightarrow3\left(a^3+a^2b+ab^2+b^3\right)>0\)
\(\Leftrightarrow3\left[a^2\left(a+b\right)+b^2\left(a+b\right)\right]>0\)
\(\Leftrightarrow3\left(a^2+b^2\right)\left(a+b\right)>0\)(đpcm)