Tìm a,b,c để: x3 +ax2 +bx +c chia cho x+2 ; x+1; x-1 đều dư 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2017
Sử dụng giả thiết và điều kiện cần của cực trị ta có
y(1) = 0; y'(-1) = 0; y(-1) = 0
Trong đó , y ' = 3 x 2 + 2 a x + b
Từ đó suy ra:
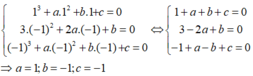
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x 3 + x 2 - x - 1
Ta có y ' = 3 x 2 + 2 x - 1 , y ' ' = 6 x + 2 . V ì y ' ' = ( - 1 ) = - 4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.
Chọn đáp án C.
K
1
CM
28 tháng 7 2019
Đáp án C
Phương pháp giải:
Chọn hệ số a, b, c hoặc đánh giá tích để biện luận số nghiệm của phương trình
Lời giải:
Cách 1. Ta có: 
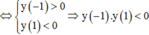
Lại có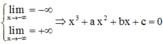 
có 3 nghiệm thuộc khoảng 
Cách 2. Chọn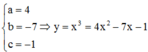 
và đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt
CM
30 tháng 8 2018
Đồ thị hàm số có hai điểm cực đại là A, B nên f ' (-2) = 0 nên 12 - 4a + b = 0 và f ' (2) = 0 nên 12 + 4a + b = 0.
Do A thuộc đồ thị hàm số nên 16 = -8 + 4a - 2b + c.
Giải hệ gồm ba phương trình trên ta thu được a = c = 0; b = -12. Suy ra a + b + c = -12
Đáp án A
1 tháng 1 2017
(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
- Kẻ bảng, trên dòng đầu tiên ghi các hệ số của đa thức đầu tiên, ở đây là \(1,0,a,b,c\).
- Theo định lí Bezout thì đa thức sẽ có nghiệm bội 3 là số 3, do đó chừa một cột bên tay trái ghi nghiệm (là số 3).
- Hạ hệ số (là 1) xuống, thực hiện quy tắc "nhân ngang cộng chéo" (nhân từ nghiệm qua rồi cộng chéo lên).
- VD: 3 nhân 1 cộng 0 là 3, viết 3. 3 nhân 3 cộng a là a+9, viết a+9. 3 nhân (a+9) cộng b là 3a+b+27, viết 3a+b+27...
- Để 3 là nghiệm của đa thức thì hệ số cuối cùng là 0, tức là \(9a+3b+c+27=0\).
- Tự làm tiếp, ra thêm 2 cái phương trình nữa...
Gọi thương của x3 +ax2 +bx +c chia cho x+2 ; x+1; x-1 lần lượt là
f(x),q(x) ,p(x) ta đc
x3 +ax2 +bx +c =(x+2).f(x)+8 (1)
x3 +ax2 +bx +c =(x+1).q(x)+8 (2)
x3 +ax2 +bx +c =(x-1).p(x)+8 (3)
Các đẳng thức (1),(2),(3) luôn đúng
*Với x=-2 từ (1) ta đc
-8+4a-2b +c=8
=>4a-2b+c=16 (*)
*Với x=-1 từ (2) ta đc
-1+a-b+c=8
=> a-b+c=9 (**)
*Với x=1 từ (3) ta đc
1+a+b+c=8
=> a+b+c=7 (***)
từ (*) ; (**) ; (***) ta đc
a=2 . b=-1 , c=6