Xin vui lòng giúp em giải 2 bài toán sau ạ. Em xin cảm ơn thật nhiều!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
TN
GIÚP EM BÀI TẬP TOÁN 9VỚI Ạ .EM ĐANG KIỂM TRa.CỨU EM VỚI MỌI Người.!!
Em xin cảm ơn rất nhiều luôn ạ
1
25 tháng 10 2021
Câu 5:
\(x=\dfrac{6^2}{10}=3.6\left(cm\right)\)
y=10-3,6=6,4(cm)
28 tháng 10 2021
\(P=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{x-4}.\dfrac{x-4}{-2\sqrt{x}}=\dfrac{2x}{-2\sqrt{x}}=-\sqrt{x}\)
\(P=-\sqrt{x}=-\sqrt{4}=-2\left(đpcm\right)\)
NQ
4
CG
1
F
17 tháng 4 2022
\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)
HH
3
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(a,\dfrac{x}{9}=\dfrac{5}{3}\\ \Leftrightarrow x=9\cdot\dfrac{5}{3}\\ \Leftrightarrow x=15\\ b,\dfrac{17}{x}=\dfrac{85}{105}\\ \Leftrightarrow x=17\cdot\dfrac{105}{85}\\ \Leftrightarrow x=21\\ c,\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\\ \Leftrightarrow\dfrac{x}{8}=\dfrac{1}{2}\\ \Leftrightarrow x=4\\ d,\dfrac{3}{x-7}=\dfrac{27}{135}\\ \Leftrightarrow x-7=15\\ \Leftrightarrow x=22\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 8 2023
\(e,\dfrac{75}{20-x}=\dfrac{3}{2}\times10\\ \Leftrightarrow\dfrac{75}{20-x}=15\\ \Leftrightarrow20-x=5\\ \Leftrightarrow x=15\\ f,\left(x-50\%\right)\times\dfrac{5}{3}=\dfrac{7}{4}-0,5\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{5}{4}\\ \Leftrightarrow x-\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x=\dfrac{5}{4}\\ g,\left(\dfrac{2}{15}+\dfrac{3}{35}+\dfrac{2}{63}\right):x=\dfrac{1}{18}\\ \Leftrightarrow\dfrac{2}{9}:x=\dfrac{1}{18}\\ \Leftrightarrow x=4\)
\(h,\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=0,6\times\dfrac{40}{6}\\ \Leftrightarrow\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=4\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6+4=6\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6=2\\ \Leftrightarrow x-\dfrac{1}{2}=12\\ \Leftrightarrow x=\dfrac{25}{2}\)
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
12 tháng 7 2017
nối 1 điểm bất kì với n-1 điểm còn lại ta đc n-1 đường thẳng=>số đường thẳng vẽ đc là:n.(n-1)
mà mỗi đường thẳng đc nhắc lại 2 lần
=>số đường thẳng vẽ đc trên thực tế là:
\(\frac{n\left(n-1\right)}{2}\)=\(\frac{2017.2016}{2}=2033136\)(đường thẳng)
vậy.......
AL
12 tháng 7 2017
Cứ 1 điểm ta lại tạo được với 2016 điểm còn lại 2016 đường thẳng.
=>Số đường thẳng có là:
2016 x 2017=4066272(đường thẳng)
Nhưng thực chất mỗi đường thẳng được nhắc lại 2 lần nên ta có:
Số đường thẳng thật sự là:
4066272 :2=2033136(đường thẳng)
Vật cho 2017 điểm trong đó không có 3 điểm nào thẳng hàng,ta vẽ được 2033136 đường thẳng
Học giỏi ^^
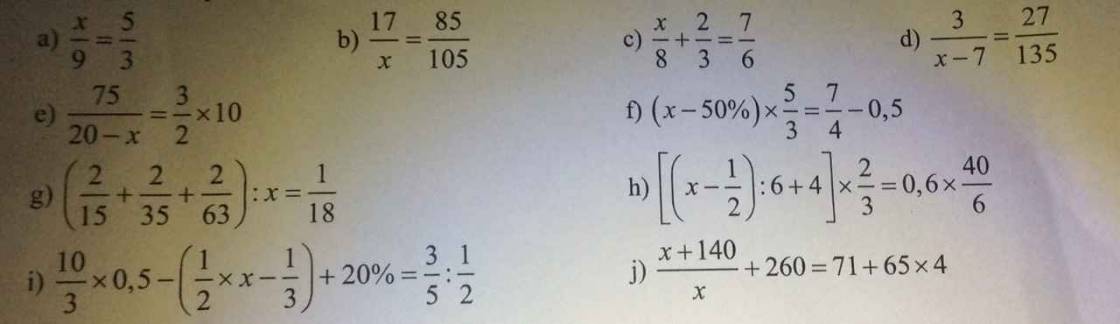
1, \(\sqrt{4x-20}-\sqrt{x+5}=\sqrt{x-5}\)ĐK : x >= 5
\(\Leftrightarrow2\sqrt{x-5}-\sqrt{x+5}-\sqrt{x-5}=0\)
\(\Leftrightarrow\sqrt{x-5}=\sqrt{x+5}\Leftrightarrow x-5=x+5\Leftrightarrow0=10\)( vô lí )
Vậy pt vô nghiệm
A B C ∝
Do \(tan.\alpha=3\Rightarrow\frac{AB}{AC}=\frac{1}{3}\)
\(\Rightarrow\frac{AB^2}{AC^2}=\frac{1}{9}\Rightarrow AB^2=\frac{AC^2}{9}=\frac{AB^2+AC^2}{1+9}=\frac{BC^2}{10}\)
\(\Rightarrow AB^2=\frac{AC^2}{9}=\frac{BC^2}{10}\Rightarrow AB=\frac{AC}{3}=\frac{BC}{\sqrt{10}}\)
Đặt \(AB=\frac{AC}{3}=\frac{BC}{\sqrt{10}}=k\)
\(\Rightarrow AB=k;AC=3k;BC=\sqrt{10}k\)
\(\Rightarrow A=sin^2a+2sina.cosa-5cos^2a\)
\(=\left(\frac{AC}{BC}\right)^2+2\frac{AC}{BC}.\frac{AB}{BC}-5\left(\frac{AB}{BC}\right)^2\)
\(=\left(\frac{3k}{\sqrt{10}k}\right)^2+2.\frac{3k}{\sqrt{10}k}.\frac{k}{\sqrt{10}k}-5.\left(\frac{k}{\sqrt{10}k}\right)^2\)
\(=\frac{9}{10}+\frac{2.3}{10}-\frac{5.1}{10}=\frac{21}{10}\)
Vậy \(A=\frac{21}{10}\)
\(\)