Δ ABC co phai là Δ can nếu các cạnh AB,AC,BC lan lượt 9,12,15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
23 tháng 3 2022
xét tam giác ABC vuông tại A ( gt)
\(AB^2+AC^2=BC^2\)
=> \(BC^2=AB^2+AC^2\)
= \(21^2+28^2=1225\)
=> BC = \(\sqrt{1225}=35\left(BC>0\right)\)
VẬY BC = 35 CM
5 tháng 11 2021
a: Xét ΔAME và ΔBMP có
\(\widehat{MAE}=\widehat{MBP}\)
AM=BM
\(\widehat{AME}=\widehat{BMP}\)
Do đó: ΔAME=ΔBMP
2 tháng 3 2016
Thấy :
\(9^2+12^2=81+144=225=15^2\)
Do đó tam giác ABC vuông tại A có cạnh huyền BC
2 tháng 3 2016
áp dụng định lý py-ta-go vào tam giác ABC ta có :
9^2+12^2=81+144=225= 15^2
vậy tam giác ABC là tam giác vuông tại A
30 tháng 1 2022
\(\widehat{B}=\widehat{C}=\dfrac{180^0-120^0}{2}=30^0\)
Gọi H là trung điểm của AB, K là trung điểm của AC
Ta có: D nằm trên đường trung trực của AB
nên DA=DB
\(\Leftrightarrow\widehat{DAH}=30^0\)
Ta có: E nằm trên đường trung trực của AC
nên EA=EC
=>\(\widehat{EAK}=30^0\)
Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AH=AK
\(\widehat{HAD}=\widehat{KAE}\)
Do đó: ΔAHD=ΔAKE
Suy ra: AD=AE
hay ΔADE cân tại A
mà \(\widehat{EAD}=60^0\)
nên ΔAED đều
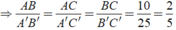
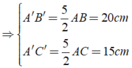
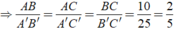
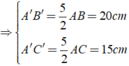
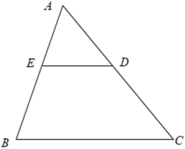
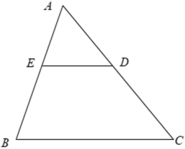
\(\Delta ABC\) không phải tam giác cân nếu AB và AC không bằng nhau.
(Theo định lý hay tính chất không nhớ rõ)
ko nhớ là ko biết coi như đáp án bạn sai