10 + nn = 37
Tìm n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 8 2018
Kiểm tra với n = 1
Giả sử đã cho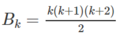 
Ta cần chứng minh
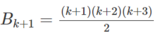
bằng cách tính
PS
3
10 tháng 2 2020
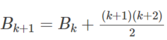
uses crt;
const n=10;
var a:array[1..n]of real;
i:integer;
nn:real;
begin
clrscr;
for i:=1 to n do
begin
write('a[',i,']='); readln(a[i]);
end;
{-------------------------xu-ly----------------------}
nn:=a[1];
for i:=1 to n do
if nn>a[i] then nn:=a[i];
writeln('phan tu nho nhat cua day la: ',nn);
readln;
end.
9 tháng 10 2022
a:
Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=-\dfrac{\left(-2\right)}{2\cdot1}=1\\y=-\dfrac{\left(-2\right)^2-4\cdot1\cdot3}{4\cdot1}=-\dfrac{4-12}{4}=2\end{matrix}\right.\)
=>Hàm số đồng biến khi x>1 và nghịch biến khi x<1
=>Trong khoảng (-1;1) thì khi x tăng thì y giảm và trong khoảng (1;2) thì khi x tăng thì y tăng
=>Khi x=1 thì f(x) min
=>\(y=1^2-2\cdot1+3=1-2+3=2\)
b: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-2\right)}{2\cdot1}=1\\y=-\dfrac{\left(-2\right)^2-4\cdot1\cdot5}{4}=-\dfrac{4-20}{4}=-\dfrac{-16}{4}=4\end{matrix}\right.\)
=>Hàm số nghịch biến khi x<1 và đồng biến khi x>1
=>Trên khoảng [2;3] thì khi x tăng thì y tăng
Do đó: Khi x=2 thì y min và x=3 thì y max
Khi x=2 thì \(y=2^2-2\cdot2+5=5\)
Khi x=3 thì \(y=3^2-2\cdot3+5=9+5-6=8\)
27 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
long long i,n,t,x,dem;
int main()
{
cin>>n;
t=0;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x>=0)
{
t=t+x;
dem++;
}
}
cout<<fixed<<setprecision(2)<<t*1.0/(dem*1.0);
return 0;
}
CM
27 tháng 11 2017
- Khi n = 1, VT = 1;
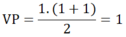
⇒ VT = VP , do đó đẳng thức đúng với n = 1.
- Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là:
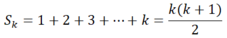
Ta phải chứng minh rằng đẳng thức cũng đúng với n = k + 1, tức là:
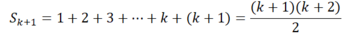
Thật vậy, từ giả thiết quy nạp ta có:
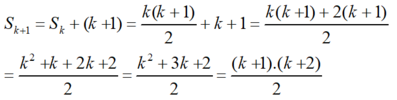
Vậy đẳng thức đúng với mọi n ∈ N*