Cho ΔABC có AB = BC. Gọi D là trung điểm của BC. Chứng minh rằng.
a) ΔADB = ΔADC
b) AD ⊥ BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

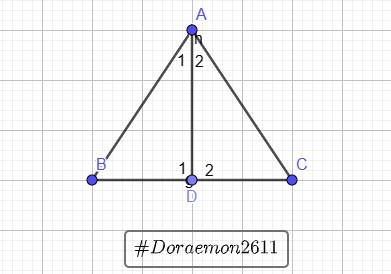
`a)` Vì `D` là trung điểm `BC=>DB=DC`
Xét `\triangle ABD` và `\triangle ACD` có:
`{:(AB=AC),(AD\text{ là cạnh chung}),(BD=CD):}}=>\triangle ABD=\triangle ACD` (c-c-c)
`b)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường phân giác của `\triangle ABC`
`=>AD` là tia phân giác của `\hat{BAC}`
`c)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường cao của `\triangle ABC`
`=>AD \bot BC`
`a,` Xét Tam giác `ABD` và Tam giác `ACD` có (bạn lưu ý ghi đúng tên của Tam giác để có các cạnh và góc tương ứng nhé)
`AB = AC (g``t)`
AD chung
`DB = DC (g``t)`
`=>` Tam giác `ABD =` Tam giác `ACD (c-c-c)`
`b,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng)
`=> AD` là tia phân giác của \(\widehat{BAC}\)
`c,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>`\(\widehat{ADB}+\widehat{ADC}=180^0\)
`=>` \(\widehat{ADB}=\widehat{ADC}=\) \(\dfrac{180}{2}=90^0\)
`=>`\(AD\perp BC\) `(đpcm)`
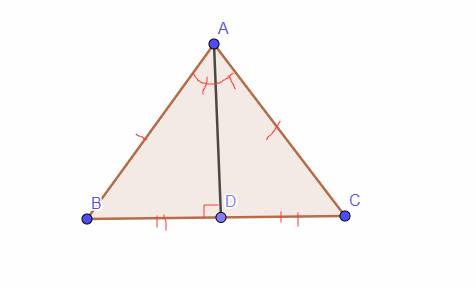

a) Xét \(\Delta ADB\) và \(\Delta ADC\) ta có:
\(\widehat{BAD}+\widehat{B}+\widehat{BDA}=180^o\)
\(\widehat{DAC}+\widehat{C}+\widehat{CDA}=180^o\)
Mà \(\widehat{B}=\widehat{C}\left(gt\right)\)(*)
\(\widehat{BAD}=\widehat{DAC}\) (AD là phân giác)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}\) (**)
AD là cạnh chung. (***)
Vậy: từ (*) (**) (***) ta có \(\Delta ADB\) = \(\Delta ADC\) (g.c.g)
b) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow AB=AC\) (2 cạnh tương ứng)
c) Vì: \(\Delta ADB\) = \(\Delta ADC\) (cm a)
\(\Rightarrow DB=DC\) (2 cạnh tương ưng)
Mà D thuộc BC (gt)
=> D là trung điểm của BC. (****)
Lại có: AD là tia phân giác góc A (*****)
Từ (****) và (*****) suy ra AD là đường trung trực của BC

a) Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
BC2= AB2 +AC2
=> BC =\(\sqrt{AB^2+AC^2}\)=\(\sqrt{5^2+12^2}\)=13 (cm)
Trả lời (Tự vẽ hình)
a) \(\Delta ABC\)vuông tại A
=> Áp dụng định lý Pi-ta-go
Ta có: \(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\)
\(\Rightarrow BC=13\left(cm\right)\)
Vậy BC=13 (cm)
b) Xét \(\Delta ABC\&\Delta ADC\)có:
AC chung (1)
\(\widehat{BAC}\)\(=\widehat{CDA}\)\(\left(=90^o\right)\left(2\right)\)
\(AB=AD\left(gt\right)\left(3\right)\)
(1)(2)(3)\(\Rightarrow\Delta ABC=\Delta ADC\)
Vậy \(\Delta ABC=\Delta ADC\left(đpcm\right)\)
c) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\hept{\begin{cases}c_1=c_2\left(cmt\right)\\BC=AE\left(gt\right)\\CEA=c_1\end{cases}\Rightarrow\Delta AEC}\)cân
Vậy \(\Delta AEC\)cân (đpcm)
\(\)

a) Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)
hay AC=4(cm)
Vậy: AC=4cm
b)Xét ΔADC vuông tại A và ΔABC vuông tại A có
CA chung
AD=AB(gt)
Do đó: ΔADC=ΔABC(hai cạnh góc vuông)
c) Xét ΔEMD và ΔBMC có
\(\widehat{EDM}=\widehat{BCM}\)(hai góc so le trong, ED//BC)
MD=MC(M là trung điểm của CD)
\(\widehat{EMD}=\widehat{BMC}\)(hai góc đối đỉnh)
Do đó: ΔEMD=ΔBMC(g-c-g)
Suy ra: ED=BC(hai cạnh tương ứng)
mà BC=CD(ΔCDA=ΔCBA)
nên ED=CD
hay ΔCDE cân tại D

a)
Sửa đề: Chứng minh ΔABM=ΔACM
Xét ΔABM và ΔACM có
AB=AC(gt)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
b) Xét ΔABM vuông tại M và ΔDCM vuông tại M có
MB=MC(M là trung điểm của BC)
AM=DM(gt)
Do đó: ΔABM=ΔDCM(hai cạnh góc vuông)
⇒\(\widehat{ABM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
A B C D
a, Xét \(\Delta ADB;\Delta ADC\) có :
\(\left\{{}\begin{matrix}AB=AC\\DB=DC\\ADchung\end{matrix}\right.\)
\(\Leftrightarrow\Delta ADB=\Delta ADC\left(c-c-c\right)\)
b, \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Leftrightarrow\widehat{BDA}=\widehat{ADC}\)
Lại có :
\(\widehat{BDA}+\widehat{ADC}=180^0\left(kềbuf\right)\)
\(\Leftrightarrow\widehat{BDA}+\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
\(\Leftrightarrow AD\perp BC\)