So sánh: 32n va 23n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
20 tháng 10 2017
cute phô mai que kết quả của bn đúng rồi, tôi thêm cách làm vào thôi.
Giải:
32n = (32)n = 9n
23n = (23)n = 8n
Mà: 8 < 9
Nên: 9n > 8n
=> 32n > 23n
NT
2
NT
4 tháng 8 2018
Hãy tích cho tui đi
Nếu bạn tích tui
Tui không tích lại đâu
THANKS
4 tháng 8 2018
Ta có \(A=3^{2n}+3=\left(3^2\right)^n+3=9^n+3\)
\(B=2^{3n}+2=\left(2^3\right)^n+2=8^n+2\)
Ta thấy \(8^n< 9^n;2< 3\Rightarrow8^n+2< 9^n+3\)
Do đó \(A>B\)
Vậy A > B
NL
1
19 tháng 7 2016
có 32n = (32)n = 9n
có 23n = (23)n = 8n
Vì 8<9 nên 8n<9n hay 23n < 32n
19 tháng 7 2016
+ Với n = 0 thì 32n = 32.0 = 30 = 1
23n = 23.0 = 20 = 1
Lúc này 32n = 23n
+ Với n khác 0, ta có: 32n = (32)n = 9n
23n = (23)n = 8n
Vì 9n > 8n
=> 32n > 23n
27 tháng 7 2016
\(3^{2n}=9^n\)
\(2^{3n}=8^n\)
Vì 8 < 9 mà n = n
=> 8n < 9n
=> 23n < 32n
19 tháng 9 2015
32n và 23n
32n=(32)n=9n
23n=(23)n=8n
Mà 8 < 9
=> 8n < 9n
=> 32n > 23n
Nhấn đúng cho mình nha, thank
2 tháng 7 2016
+ Với n = 0 => 32n = 32.0 = 30 = 1; 23n = 23.0 = 20 = 1
Vì 1 = 1
=> 32n = 23n
+ Với n khác 0; ta có: 32n = (32)n = 9n; 23n = (23)n = 8n
Vì 9 > 8
=> 9n > 8n
Ủng hộ mk nha ^_-
10 tháng 9 2020
\(3^{2n}=\left(3^2\right)^n=9^n\)
\(2^{3n}=\left(2^3\right)^n=8^n\)
Vì \(9^n>8^n,\forall n\inℕ^∗\)nên \(3^{2n}>2^{3n}\)
LT
5
XO
25 tháng 7 2019
Ta có :32n =(32)n = 9n
23n =(23)n = 8n
Vì 9 > 8 =>9n > 8n =>32n > 23n
Vậy 32n >23n
Chúc bạn học tốt !!!!
25 tháng 7 2019
32n và 22n
32n = 9n
22n = 8n
Vì 9n > 8n nên 32n >22n
*good luck*
HH
9
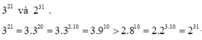
Bạn làm cụ thể đi rồi tớ cho l-i-k-e
Ta có:
32n= (32)n = 9n
23n= (23)n = 8n
Vì 9n>8n
=>32n>23n
L-i-k-e nha bạn