y=log3(m\(^2\)-x\(^2\)). Để hàm số xác định trên khoảng (-2;2) thì giá trị m phải là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 7 2019
Đáp án B
Hàm số xác định với mọi x ∈ 1 ; 2 ⇔ − x 2 + m x + 2 m + 1 > 0 ∀ x ∈ 1 ; 2 .
⇔ m > x 2 − 1 x + 2 = g x ∀ x ∈ 1 ; 2 ⇔ m > M ax 1 ; 2 g x
Xét g x = x 2 − 1 x + 2 = x − 2 + 3 x + 2 ⇒ g ' x = 1 − 3 x + 2 2 > 0 ∀ x ∈ 1 ; 2
Do đó lim x → 2 f x = 3 4 . Vậy m ≥ 3 4 là giá trị cần tìm.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)
CM
27 tháng 2 2018
Đáp án C
Ta có y ' = 2 − m x + 2 2 . Hàm số đồng biến trên từng khoảng xác định y ' > 0 , ∀ x ∈ D ⇔ 2 − m > 0 ⇔ m < 2 .
CM
9 tháng 3 2019
Tập xác định
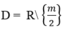
Hàm số nghịch biến trên từng khoảng
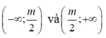
khi và chỉ khi
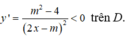
Suy ra m 2 - 4 < 0 hay -2 < m < 2. Chọn đáp án C.
CM
16 tháng 8 2019
Đáp án: D.
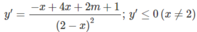
⇔ ∆ ′ = 2m + 5 ≤ 0
dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (- ∞ ; 2)
và (2; + ∞ ) khi m ≤ −5/2.
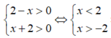
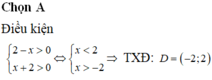
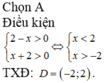
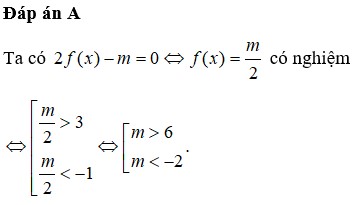
Xét \(f\left(x\right)=m-x\) (m là tham số).
\(Min_{\left[-2;2\right]}f\left(x\right)=f\left(2\right)=m-2;Max_{\left[-2;2\right]}=f\left(-2\right)=m+2\).
Để làm số xác định trên khoảng (-2;2) thì \(m-x>0\) trên khoảng (-2;2).
Suy ra \(Mix_{\left[-2;2\right]}f\left(x\right)\ge0\Leftrightarrow\) \(m-2\ge0\Leftrightarrow m\ge2\).