Tính : A = 12 + 22 + 32 + ............ + 992
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2020
a) \(=\left(127+73\right)^2=200^2=40000\)
b) \(=18^8-\left(18^8-1\right)=1\)
c) \(=\left(100+99\right)\left(100-99\right)+\left(98+97\right)\left(98-97\right)+...+\left(2+1\right)\left(2-1\right)\)
\(=100+99+98+97+...+2+1=5050\)
d) biến đổi thành \(20^2-19^2+18^2-17^2+..+2^2-1^2\)
rồi giải ra như trên
1 tháng 11 2023
a:
Số số hạng trong dãy M là:
(1002-12):10+1=100(số)
=>Sẽ có 50 cặp (1002;992); (982;972);....;(22;12) có hiệu bằng 10
\(M=1002-992+982-972+...+22-12\)
\(=\left(1002-992\right)+\left(982-972\right)+...+\left(22-12\right)\)
\(=10+10+...+10\)
=10*50=500
b: \(N=\left(202+182+...+42+22\right)-\left(192+172+...+32+12\right)\)
\(=\left(202-192\right)+\left(182-172\right)+...+\left(22-12\right)\)
=10+10+...+10
=10*10=100
KN
2
29 tháng 6 2023
\(100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
\(=199+195+...+3\)
Số lượng số hạng:
\(\left(199-3\right):4+1=50\) (số hạng)
Tổng:
\(\left(3+199\right)\times50:2=5050\)
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Lời giải:
$=(100^2-99^2)+(98^2-97^2)+....+(2^2-1^2)$
$=(100-99)(100+99)+(98-97)(98+97)+...+(2-1)(2+1)$
$=100+99+98+97+...+2+1=100(100+1):2=5050$
LN
1
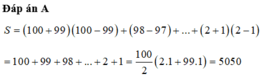
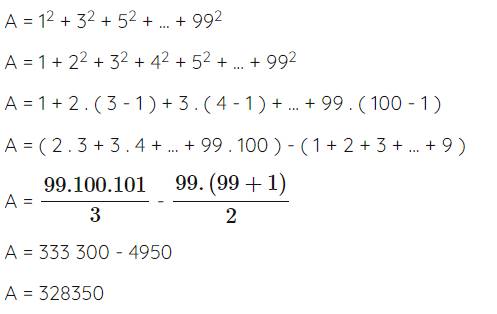
A = 1.1+2.2+3.3+...+99.99
=>A= 1.(2-1)+2.(3-1)+3.(4-1)+...+99.(100-1)
=>A=1.2-1+2.3-2+3.4-3+...+99.100-99
=>A=(1.2+2.3+3.4+......+99.100)-(1+2+3+...+99)
Đặt S =1.2+2.3+3.4+...+99.100
=>3S= 1.2.3+2.3.3+3.4.3+....+99.100.3
=>3S= 1.2.3+2.3.(4-1)+3.4.(5-2)+.....+99.100.(101-98)
=>3S =1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+.....+99.100.101-98.99.100
=>3S= 99.100.101=999900
=>S= 999900:3=333300
=>A =333300 -(99+1).99:2
=>A=333300-4950
=>A=328350
A= 12 + 22 + 32 + ... + 992 + 1002
A = 1 + 2(1 + 1) + 3(2 + 1) +... + 99(98 + 1) + 100(99 + 1)
A = 1 + 1.2 + 2 + 2.3 + 3 +... + 98.99 + 99 + 99.100 + 100
A = (1.2 + 2.3 + 3.4 +... + 99.100) + (1 + 2 + 3 +... + 99 + 100)
A = 333300 + 5050
A = 338050
Vậy A = 338050