(3,5 điểm) Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.
1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.
2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và...
Đọc tiếp
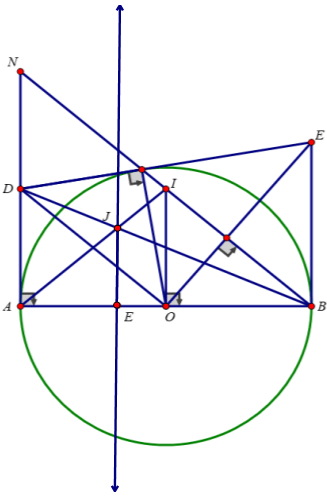
(3,5 điểm) Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.
1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.
2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và vuông góc với BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.
3) Chứng minh H là trực tâm tam giác ABC
4) Khi đường thẳng d thay đổi và thỏa mãn điều kiện của đề bài, điểm H di động trên đường nào
Giúp mình với ạ!
2/
Áp dụng tính chất đường kính đi qua trung điểm dây cung ta được \(OM\perp BC\)
Vì \(AH\perp BC\left(gt\right)\)
Nên \(AH\)//\(OM\)
Xét \(\Delta AHN\) có \(OA=ON\) và \(AH\)//\(OM\)
Suy ra \(OM\) là đường trung bình của \(\Delta AHN\)
nên \(MN=MH\)
Xét tứ giác \(BHCN\) có \(\left\{{}\begin{matrix}MB=MC\left(gt\right)\\MN=MH\left(cmt\right)\end{matrix}\right.\) suy ra tứ giác \(BHCN\) là hình bình hành (đpcm)
3/
Xét \(\Delta BAN\) vuông tại \(B\) (cạnh huyền là đường kính)
hay \(BN\perp AB\) (1)
Mà \(CH\)//\(BN\) (2 cạnh đối hình bình hành) (2)
Từ (1) (2) suy ra \(CH\perp AB\)
Mà \(AH\perp BC\left(gt\right)\)
Do vậy H là trực tâm \(\Delta ABC\) (đpcm)