đề bài : Tính
e cần cả cách giải chi tiết ạ😢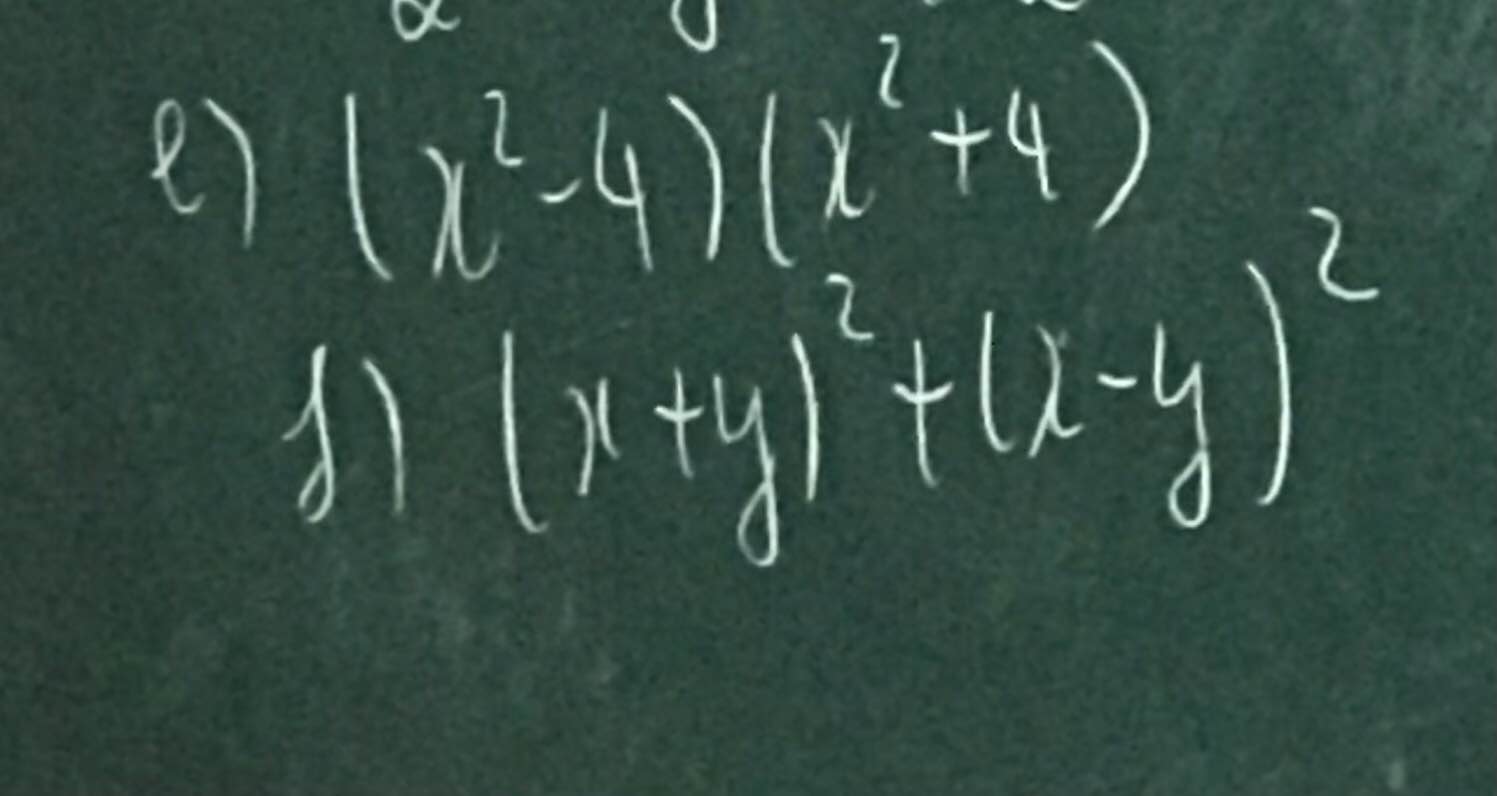
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
4
Những câu hỏi liên quan
24 tháng 8 2021
a: Ta có: \(\left(12x-5\right)\left(4x-1\right)+\left(3x-7\right)\left(1-16x\right)=81\)
\(\Leftrightarrow48x^2-32x+5+3x-48x^2-7+112x=81\)
\(\Leftrightarrow83x=83\)
hay x=1
b: Ta có: \(\left(4x-5\right)\left(3x-2\right)-\left(2x+6\right)\left(6x-1\right)=17\)
\(\Leftrightarrow12x^2-8x-15x+10-12x^2+2x-36x+6=17\)
\(\Leftrightarrow-57x=13\)
hay \(x=-\dfrac{13}{57}\)
DT
10
20 tháng 2 2022
Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
d: \(AH^2-AN^2=HN^2\)
\(BH^2-BM^2=MH^2\)
mà HN=MH
nên \(AH^2-AN^2=BH^2-BM^2\)
hay \(AH^2+BM^2=BH^2+AN^2\)
KB
1 tháng 5 2022
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 3 2023
Do (d) đi qua C và D, thay tọa độ C và D vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.\left(-1\right)+b=1\\a.\left(-2\right)+b=-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\-2a+b=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)
Phương trình (d) có dạng: \(y=4x+5\)
2 tháng 7 2023
\(E-2\overline{yzt}=\overline{xz}\)
=>1000x+100y+10z+t-200y-20z-20t=10x+z
=>990x-100y-11z-19t=0
=>\(\left(x,y,z,t\right)\in\varnothing\)
30 tháng 1 2016
bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok
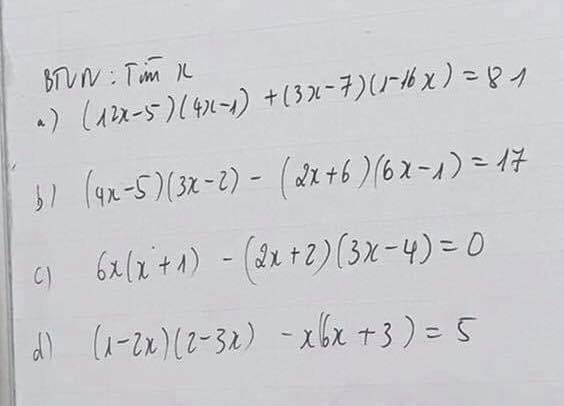
e) \(\left(x^2-4\right)\left(x^2+4\right)=\left(x^2\right)^2-4^2=x^4-16\)
f) \(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2\)
(x2 - 4)(x2 + 4)
Áp dụng hằng đẳng thức số 3, ta có:
<=> \(\left[\left(x^2\right)^2-4^2\right]\)
<=> (x4 - 16)
Mik làm chi tiết rồi, có gì ko hiểu bảo mik