chứng tỏ rằng tổng ab + ba chia hết cho 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
4
7 tháng 8 2015
ab+ba
=10a+b+10b+a
=11a+11b
=11(a+b)chia hết cho 11
=>ab+ba chia hết cho 11
7 tháng 8 2015
Ta có: ab+ba = 10a+b + 10b+a = (10a+a)+(10b+b) = 11a + 11b = 11(a+b) luôn chia hết cho 11
Tick đúng cho mk nha!!!!!!!!!!
14 tháng 10 2019
1. Chứng tỏ rằng: ab + ba chia hết cho 11:
Ta có: ab+ba=10a+b+10b+a=11a+11b=11(a+b)
Vì \(11\left(a+b\right)⋮11\)
\(\Rightarrow ab+ba⋮11\)
Chứng tỏ rằng: ab - ba chia hết cho 9
Ta có: ab-ba=10a+b-10b-a=9a-9b=9(a-b)
vì \(9\left(a-b\right)⋮9\)
\(\Rightarrow ab-ba⋮9\)
XO
14 tháng 10 2019
1. a) Ta có : ab + ba = (a0 + b) + (b0 + a)
= (10a + b) + (10b + a)
= 10a + b + 10b + a
= (10a + a) + (b + 10b)
= 11a + 11b
= 11(a + b) \(⋮\)11
=> ab + ba \(⋮\)11 (ĐPCM)
b) Ta có : ab - ba = (a0 + b) - (b0 + a)
= (10a + b) - (10b + a)
= 10a + b - 10b - a
= (10a - a) - (10b - b)
= 9a - 9b
= 9(a - b) \(⋮\)9
=> ab + ba \(⋮\)9 (ĐPCM)
2) Gọi 3 số tự nhiên liên tiếp là a ; a + 1 ; a + 2
Khi đó a + a + 1 + a + 2
= 3a + 3
= 3(a + 1) \(⋮\)3 (ĐPCM)
3)
Gọi 3 số tự nhiên liên tiếp là a ; a + 1 ; a + 2
Khi đó a + a + 1 + a + 2
= 3a + 3
= 3(a + 1)
=> Tổng của 3 số liên không chia hết cho 4 (ĐPCM)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
31 tháng 8 2021
a/ \(\overline{ab}+\overline{ba}=10a+b+10b+a=11a+11b=11\left(a+b\right)⋮11\)
b/ \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b=9\left(a-b\right)⋮9\)
c/ \(\overline{abba}=1001a+110b=11.91.a+11.10.b=11\left(91a+10b\right)⋮11\)
18 tháng 10 2017
a) Theo bài ra ta có:
abcabc = 1000abc + abc
= ( 1000 +1)abc
=1001abc.
Vì : 1001 chia hết cho 11 => abcabc chia hết cho 11.
1001 chia hết cho 7 => abcabc chia hết cho 7.
1001 chia hết cho 13 => abcabc chia hết cho 13.
=> Điều phải chứng minh.
b) Ta có:
ab+ba= 10a+b+10b+a=11a+11b=11(a+b) chia hết cho 11.
=> Đpcm.
c)Giả sử 9a+7b chia hết cho 11,ta có:
9(2a+4b)-2(9a+7b)= 18a+36b-(18a+14b)=18a+36b-18a-14b=36b-14b=(36-14)b=22b
Vì 22 chia hết cho 11 => 22b chia hết cho 11.
Mà 9a+7b chia hết cho 11 => 2(9a+7b) chia hết cho 11.
=> 9(2a+4b) chia hết cho 11.
Vì UWCLN(9;11)=1 => 2a+4b chia hết cho 11.
=> Đpcm.
k tớ nha <3
5 tháng 11 2018
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
TT
2
MM
20 tháng 12 2015
ab=10.a+b
ba=10.b+a
ab+ba=11.a-11.b=11.(a-b)=> ab+ba chia hết cho 11
20 tháng 12 2015
cái đầu thiếu đề (không có dữ liệu chính)
Ta có: ab + ba = (10a.1b) + (10b.1a)
=> (1b+10b).(1a+10a)
= 11b + 11a
= 11.2.ab chia hết cho 11
=> đpcm
CM
17 tháng 6 2018
a, Gọi ba số tự nhiên liên tiếp là: a; a+1; a+2 tổng của ba số này bằng: a+a+1+a+2 = 3a + 3 = 3(a+1) là một số chia hết cho 3.
b, Gọi bốn số tự nhiên liên tiếp là: a; a+1; a+2; a+3 tổng của bốn số này bằng: a+a+1+a+2+a+3 = 4a+6, là một số chia không hết cho 4 vì 4a ⋮ 4 và 6 không chia hết cho 4
c, Ta có: a b - b a = 10 a + b - 10 b + a = 9a - 9b = 9(a - b) với a > b
Mà 9(a - b) ⋮ 9 nên a b - b a ⋮ 9
d, Ta có: a b c d = 100 a b + c d = 99 a b + a b + c d
Mà 99 a b ⋮ 11 và a b + c d ⋮ 11 (đề bài), nên a b c d ⋮ 11
14 tháng 10 2018
a, gọi 3 số tự nhiên liên tiếp đó là : a; a + 1; a + 2
tổng của chúng là :
a + a + 1 + a + 2
= (a + a + a) + (1 + 2)
= 3a + 3
= 3(a + 1) ⋮ 3 (đpcm)
b, trong 2 số tự nhiên liên tiếp chắc chắn có 1 số chia hết cho 2
=> tích của chúng chia hết chô 2 (đpcm)
c, gọi số tự nhiên có 3 chữ số giống nhau là : aaa (a là chữ số)
aaa = a.111 = a.3.37 ⋮ 37 (đpcm)
d, ab + ba
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b) ⋮ 11 (đpcm)
NV
14 tháng 10 2018
d, ab + ba
= 10a + b + 10b + a
= a ( 10 + 1) + b(10+1)
= a.11 + b.11
= ( a + b ).11 \(⋮\)11
Vậy ab + ba \(⋮\)11
Hok tốt
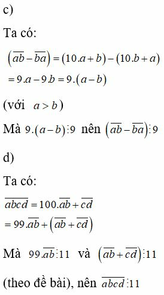
ab+ba = 10a+b+10b+a = 11a+11b=11(a+b) chia hết cho 11
=> dpcm