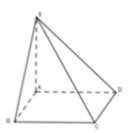
câu 7:Cho hình chóp S.ABCD có đáy là hình vuông cạnh a; hình chiếu vuông hóc của S trên ( ABCD) trùng voie trung điểm của AD và gọi M là trung điểm DC. Cạnh bên SB hợp với đáy mốt góc 60 độ . tính thể tích của khối chóp S.ABM
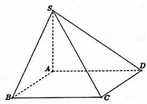
Câu8: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a ; tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Cạnh bên SB hợp với đáy một góc 60 độ . Tính thể tích của khối chóp S.ABC
giúp tôi tặng GP




Câu 7:
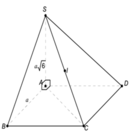
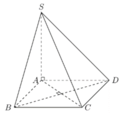
Gọi $H$ là trung điểm của $AD$ suy ra \(SH\perp (ABCD)\)
Khi đó \(60^0=(SB,(ABCD))=(SB,BH)=\angle SBH\)
\(\Rightarrow \frac{SH}{HB}=\tan 60=\sqrt{3}\)
Sử dụng công thức Pitago: \(HB=\sqrt{AB^2+AH^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{\sqrt{5}}{2}a\)
\(\Rightarrow SH=BH\sqrt{3}=\frac{\sqrt{15}a}{2}\)
Có \(S_{ABM}=\frac{d(M,AB).AB}{2}=\frac{a^2}{2}\)
\(\Rightarrow V_{S.ABM}=\frac{1}{3},SH.S_{ABM}=\frac{1}{3}.\frac{\sqrt{15}a}{2}.\frac{a^2}{2}=\frac{\sqrt{15}a^3}{12}\)
Câu 8:
Kẻ \(SH\perp AC\). Vì \((SAC)\perp (ABC)\Rightarrow SH\perp (ABC)\)
Khi đó , \(\angle (SB,(ABC))=\angle (SB,BH)=\angle SBH=60^0\)
\(\Rightarrow \frac{SH}{BH}=\tan 60=\sqrt{3}\)
Vì $SAC$ cân tại $S$ nên $H$ là trung điểm của $AC$
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{a^2-\frac{a^2}{4}}=\frac{\sqrt{3}a}{2}\)
\(\Rightarrow SH=\frac{3a}{2}\)
\(\Rightarrow V_{S.ABC}=\frac{1}{3}.SH.S_{ABC}=\frac{1}{3}.\frac{3a}{2}.\frac{BH.AC}{2}=\frac{1}{3}.\frac{3}{2}a.\frac{\sqrt{3}a^2}{4}=\frac{\sqrt{3}a^3}{8}\)