Tìm m để hàm số: y=x3-3mx2+(m2-1)x +2 đạt cực đại tại 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 11 2017
Chọn B
y ' = 3 x 2 - 6 m x + m 2 - 1 ; y ' ' = 6 x - 6 m
Hàm số đạt cực đại tại x = 2 khi
15 tháng 9 2023
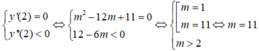
\(y=x^3-3mx^2+\left(m-1\right)x+2\)
\(y'=3x^2-6mx+m-1\)
\(y''=6x-6=6\left(x-1\right)\)
Để hàm số trên đạt cực trị tại \(x_o=2\) khi và chỉ khi
\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)>0\end{matrix}\right.\) \(\)
\(\Leftrightarrow\left\{{}\begin{matrix}12-12m+m-1=0\\6\left(2-1\right)=6>0\left(luôn.đúng\right)\end{matrix}\right.\)
\(\Leftrightarrow11m=11\)
\(\Leftrightarrow m=1\)
Vậy với \(m=1\) thỏa yêu cầu đề bài.
CM
7 tháng 4 2017
Đáp án B
Ta có: f ' x = 3 x 2 − 6 m x + 3 m 2 − 1 . Để hàm số đạt cực đại tại x 0 = 1 thì điều kiện đầu tiên là: f ' 1 = 0 ⇔ m = 0 m = 2
Nếu m = 0 thì f ' x = 3 x 2 − 3 , f ' ' x = 6 x ⇒ f ' ' 1 = 6 > 0 ⇒ x = 1 là điểm cực tiểu.
Nếu m = 2 thì f ' x = 3 x 2 − 12 x + 9 ⇒ f ' ' x = 6 x − 12 ⇒ f ' ' 1 < 0 ⇒ x = 1 là điểm cực đại.
CM
19 tháng 12 2018
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 
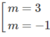
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
CM
24 tháng 10 2017
Đáp án A
Ta có: y = x 2 − 3 x + 2 x 2 − 1 = x − 1 x − 2 x − 1 x + 1 = x − 2 x + 1 ⇒
Đồ thị hàm số có 1 TCĐ.
CM
7 tháng 8 2018
Đáp án là C.
• y ' = 3 x 2 − 6 m x + 3 m 2 − 1 ; y ' ' = 6 x − 6 m
• Hàm số đạt cực đại tại x = 1 thì:
y ' 1 = 0 y ' ' 1 < 0 ⇔ 3 m 2 − 6 m = 0 6 − 6 m < 0 ⇔ m = 0 v m = 2 m > 1 ⇒ m = 2.
PT
Tìm giá trị của tham số m để hàm số y = −( m 2 + 6m) x 3 /3 − 2m x 2 + 3x + 1 đạt cực đại tại x = -1
1
CM
23 tháng 9 2018
y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = − m + 1 2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − m + 1 2 + 4 = 0 ⇔ m + 1 2 = 4
⇔ 
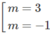
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
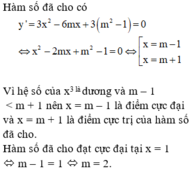
Lời giải:
Ta có \(y=x^3 -3mx^2+(m^2-1)x+2\)
\(\Rightarrow y'=3x^2-6mx+(m^2-1)\)
Để hàm số đạt cực trị tại $x=2$ thì phương trình \(y'=0\) phải có nghiệm $x=2$
\(\Leftrightarrow 3.2^2-6.m.2+m^2-1=0\)
\(\Leftrightarrow m^2-12m+11=0\Leftrightarrow m=1\) hoặc $m=11$
TH1: \(m=1\Rightarrow y'=3x^2-6x=0\Leftrightarrow x=0\) hoặc $x=2$
Lập bảng biến thiên ta thấy \(y_{\text{ct}}\) tại $x=2$ chứ không phải cực đại (loại)
TH2: \(m=11\Rightarrow y'=3x^2-66x+120=0\Leftrightarrow x=20\) hoặc \(x=2\)
Lập bảng biến thiên ta thấy \(y_{\text{cđ}}\) tại $x=2$ (thỏa mãn)
Vậy $m=11$