cau 44 trang 92 toan lop 8(hinh)
giai dum mk nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)

Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8

A B C K H I
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)


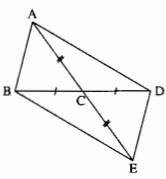
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)

Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)
Câu 44 : Trang 92 sgk toán 8 tập 1
( Bn xem có đúng bài này )
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF
Theo giả thiết ta có hình sau:
A B C D E F
Do E, F là trung điểm của AD và BC
=> DE = 12AD và BF = 12BC.
Mặt khác ABCD là hình bình hành => AD = BC
=> DE = BF
Xét tứ giác BEDF có:
DE // BF ( vì AD // BC)
DE = BF ( cmt )
=> BEDF là hình bình hành.
=> BE = DF (đpcm)