phân tích đa thức sau thành nhân tử (\(\left(x^2+4x+3\right)\left(x^2+12x+35\right)+15\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2023
\(a.\) \(ax^2-a^2x-x+a\)
\(=\left(ax^2-a^2x\right)-\left(x-a\right)\)
\(=ax\left(x-a\right)-\left(x-a\right)\)
\(=\left(ax-1\right)\left(x-a\right)\)
\(b.\) \(18x^3-12x^2+2x\)
\(=2x\left(9x^2-6x+1\right)\)
\(=2x\left(3x-1\right)^2\)
\(c.\) \(x^3-5x^2-4x+20\)
\(=\left(x^3-5x^2\right)-\left(4x-20\right)\)
\(=x^2\left(x-5\right)-4\left(x-5\right)\)
\(=\left(x^2-4\right)\left(x-5\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x-5\right)\)
\(d.\) \(\left(x+7\right)\left(x+15\right)+15\)
\(=x^2+15x+7x+105+15\)
\(=x^2+22x+120\)
\(=\left(x+10\right)\left(x+12\right)\)
2 tháng 11 2017
\(P\left(x\right)=\left(4x+1\right)\left(12x-1\right)\left(3x+2\right)\left(x+1\right)-4\)
\(=\left[\left(4x+1\right)\left(3x+2\right)\right].\left[\left(12x-1\right)\left(x+1\right)\right]-4\)
\(=\left(12x^2+8x+3x+2\right).\left(12x^2+12x-x-1\right)-4\)
\(=\left(12x^2+11x+2\right).\left(12x^2+11x-1\right)-4\)
Đặt \(12x^2+11x=t\), ta có:
\(\left(t+2\right)\left(t-1\right)-4\)
\(=t^2-t+2t-2-4=t^2+t-6\)
\(=t^2-2t+3t-6\)
\(=t\left(t-2\right)+3\left(t-2\right)=\left(t-2\right)\left(t+3\right)\)
Thay \(t=12x^2+11x\), ta được:
\(P\left(x\right)=\left(12x^2+11x-2\right)\left(12x^2+11x+3\right)\)
Đs...
27 tháng 10 2018
Đặt \(A=\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(A=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x+10=y\)
\(\Rightarrow\)\(A=y.\left(y+2\right)-24\)
\(A=y^2+2y+1-25\)
\(A=\left(y+1\right)^2-5^2\)
\(A=\left(y+1-5\right)\left(y+1+5\right)\)
\(A=\left(y-4\right)\left(y+6\right)\)
\(\Rightarrow A=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(A=\left[\left(x^2+x\right)+\left(6x+6\right)\right].\left(x^2+7x+16\right)\)
\(A=\left[x.\left(x+1\right)+6.\left(x+1\right)\right].\left(x^2+7x+16\right)\)
\(A=\left(x+1\right).\left(x+6\right).\left(x^2+7x+16\right)\)
27 tháng 10 2018
Đặt \(B=\left(4x+1\right)\left(12x-1\right)\left(3x+2\right)\left(x+1\right)-4\)
\(B=\left(12x^2+11x+2\right)\left(12x^2+11x-1\right)-4\)
Đặt \(12x^2+11x-1=a\)
\(\Rightarrow B=a.\left(a+3\right)-4\)
\(B=a^2+3a-4\)
\(B=\left(a^2-a\right)+\left(4a-4\right)\)
\(B=a.\left(a-1\right)+4.\left(a-1\right)\)
\(B=\left(a-1\right)\left(a+4\right)\)
\(\Rightarrow B=\left(12x^2+11x-2\right)\left(12x^2+11x+3\right)\)
26 tháng 8 2015
=(4x+1)(3x+2)(12x-1)(x+1)-4
=(12x2+11x+2)(12x2+11x-1)-4
đặt a=12x2+11x+2
khi đó đa thức trở thành:
a(a-3)-4
=a2-3a-4
=a2+a-4a-4
=a(a+1)-4(a+1)
=(a+1)(a-4)
thay x vào là ok
15 tháng 9 2021
\(A=4x^2+6x=2x\left(2x+3\right)\)
\(B=\left(2x+3\right)^2-x\left(2x+3\right)=\left(2x+3\right)\left(2x+3-x\right)=\left(2x+3\right)\left(x+3\right)\)
\(C=\left(9x^2-1\right)-\left(3x-1\right)^2=\left(3x-1\right)\left(3x+1\right)-\left(3x-1\right)^2=\left(3x-1\right)\left(3x+1-3x+1\right)=2\left(3x+1\right)\)
\(D=x^3-16x=x\left(x^2-16\right)=x\left(x-4\right)\left(x+4\right)\)
\(E=4x^2-25y^2=\left(2x-5y\right)\left(2x+5y\right)\)
\(G=\left(2x+3\right)^2-\left(2x-3\right)^2=\left(2x+3-2x+3\right)\left(2x+3+3x-3\right)=6.4x=24x\)
15 tháng 9 2021
\(A=2x\left(2x+3\right)\\ B=\left(2x+3\right)\left(2x+3-x\right)=\left(2x+3\right)\left(x+3\right)\\ C=\left(3x-1\right)\left(3x+1\right)-\left(3x-1\right)^2\\ =\left(3x-1\right)\left(3x+1-3x+1\right)\\ =2\left(3x-1\right)\\ D=x\left(x^2-16\right)=x\left(x-4\right)\left(x+4\right)\\ E=\left(2x-5y\right)\left(2x+5y\right)\\ G=\left(2x+3-2x+3\right)\left(2x+3+2x-3\right)\\ =24x\)
TN
11 tháng 7 2016
a)2(x-3)+12-4x
=x2(x-3)-4(x-3)
=(x2-4)(x-3)
=(x2-22)(x-3)
=(x+2)(x-2)(x-3)
b)x3-4x2-12x+27
=x3-7x2+9x+3x2-21x+27
=x(x2-7x+9)+3(x2-7x+9)
=(x+3)(x2-7x+9)
11 tháng 7 2016
a)\(x^2\left(x-3\right)+12-4x\)
\(=x^2\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x^2-2^2\right)\left(x-3\right)\)
\(=\left(x+2\right)\left(x-2\right)\left(x-3\right)\)
S
28 tháng 6 2018
1/
a, x2+36=12x
<=>x2-12x+36=0
<=>(x-6)2=0
<=>x-6=0
<=>x=6
b, 5x(x-3)+3-x=0
<=>5x(x-3)-(x-3)=0
<=>(5x-1)(x-3)=0
<=>\(\orbr{\begin{cases}5x-1=0\\x-3=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{5}\\x=3\end{cases}}}\)
2/ Sửa đề x2z2 = y2z2
Đặt \(A=4x\left(x+y\right)\left(x+y+z\right)\left(x+z\right)+y^2z^2=4x\left(x+y+z\right)\left(x+y\right)\left(x+z\right)+y^2z^2\)
\(=4\left(x^2+xy+xz\right)\left(x^2+xz+xy+yz\right)+y^2z^2\)
Đặt x2+xy+xz=t, ta có
\(A=4t\left(t+yz\right)+y^2z^2=4t^2+4tyz+y^2z^2=\left(2t+yz\right)^2=\left(2x^2+2xy+2xz+y^2z^2\right)^2\ge0\)
15 tháng 8 2016
Với x = -3 ta có -27-4*9+ 36+27=0 do đó đa thức chứa nhân tử x+3
Ta có: x^3 -4x^2-12x+27 = x^3 +3x^2 -7x^2-21x+9x+27 =(x^3 +3x^2)-(7x^2+21x) + (9x+27) =x^2(x+3) -7x(x+3)+ 9(x+3)=(x+3)(X^2 - 7x+9)
* Xét x^2 -7x + 9 = x^2 - 2x.7/2 +49/4-49/4+9 = (x-7/2)^2 -13/4 =(x-7/2- √13/2)(x-7/2+√13/2)
Vậy: x^3 -4x^2-12x+27 = (x+3)(x-7/2)^2 -13/4 =(x-7/2- √13/2)(x-7/2+√13/2)
k cho mình nha
LT
2
6 tháng 1 2018
Ta có (6x+5)2(3x+2)(x+1)-35
= (36x2+60x+25)(3x2+5x+2)-35 (1)
Đặt a=3x2+5x+2
=> 12a+1= 12(3x2+5x+2)+1 =36x2+60x+25
Thay a=3x2+5x+2 vào (1) ta được
(12a+1).a-35=12a2+a-35
= 12a2-20a+21a-35
= 4a(3a-5)+7(3a-5)
= (3a-5)(4a+7) (2)
Thay 3x2+5x+2=a vào (2) ta được
(9x2+15x+6-5)(12x2+20x+8+7)
= (9x2+15x+1)(12x2+20x+15)
7 tháng 1 2018
Ta có: \(\left(6x+5\right)^2\left(3x+2\right)\left(x+1\right)-35\)
\(=\left(36x^2+60x+25\right)\left(3x^2+5x+2\right)-35\)(1)
Đặt \(3x^2+5x+2=y\)
\(\left(1\right)=\left(12y+1\right)y-35\)
\(=12y^2+y-35\)
\(=\left(3y-5\right)\left(4y+7\right)\)
\(=\left(9x^2+15x+1\right)\left(12x^2+20x+15\right)\)
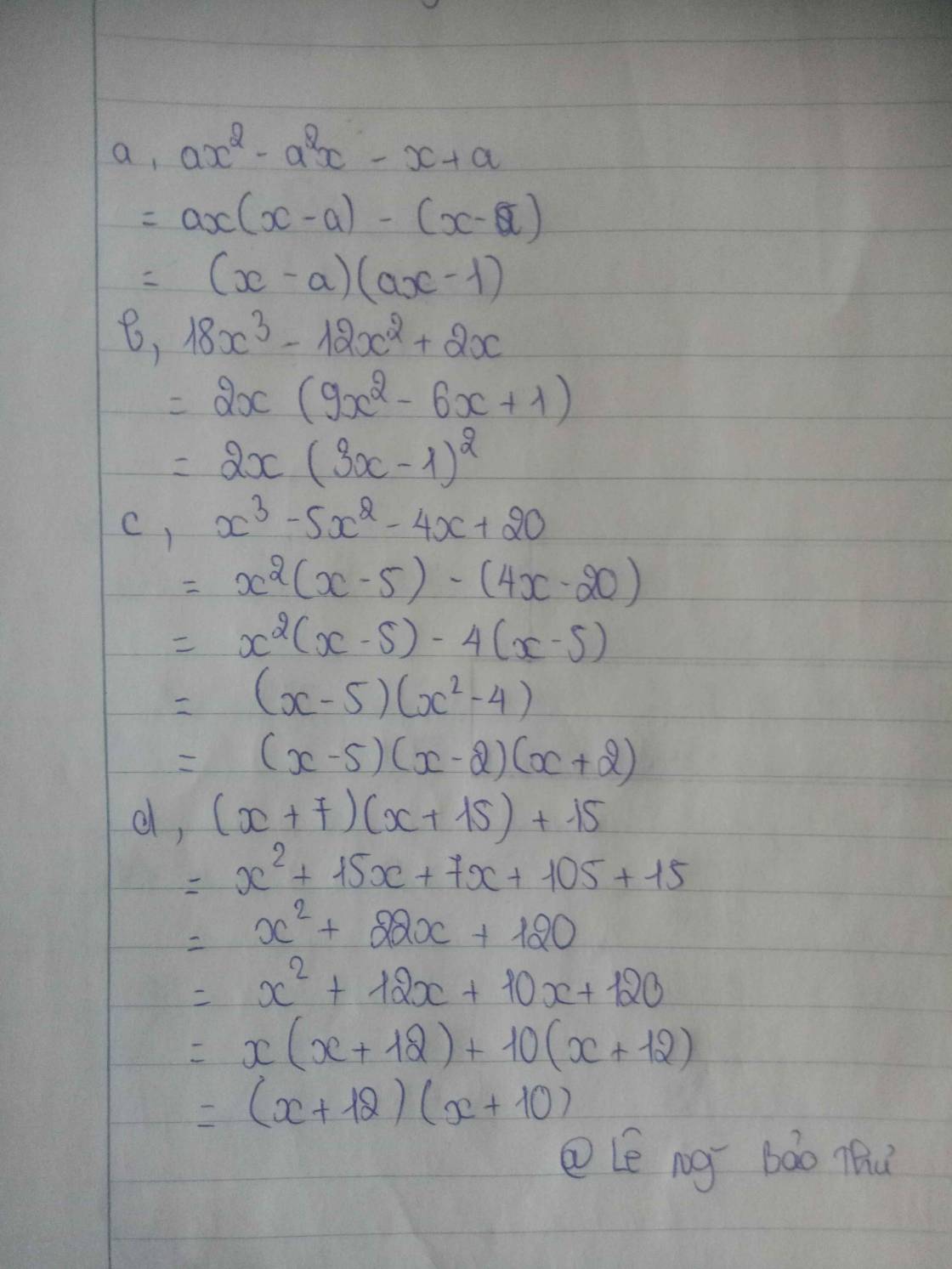
\(\left(x^2+4x+3\right)\left(x^2+12x+35\right)+15\)
\(=\left(x^2+2.x.2+2^2-1\right)\left(x^2+2.x.6+6^2-1\right)+15\)
\(=\left[\left(x+2\right)^2-1\right]\left[\left(x+6\right)^2-1\right]+15\)
\(=\left[\left(x+2\right)^2-1^2\right]\left[\left(x+6\right)^2-1^2\right]+15\)
\(=\left(x+2-1\right)\left(x+2+1\right)\left(x+6-1\right)\left(x+6+1\right)+15\)
\(=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)
\(=\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+15\)
\(=\left(x^2+7x+x+7\right)\left(x^2+5x+3x+15\right)+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
mk chỉ lm đc đến đây thôi nha bn @♂ Batman ♂