Cho \(\Delta ABC;Â=90^0\) lấy các canh AB, AC là cạnh huyền dựng ra phía ngoài của \(\Delta ABC\) các \(\Delta\) vuông cân \(ADB\) và \(\Delta AEC\) . Gọi M là trung điểm của BC, DM cắt AB tại F, EM cắt AC tại K. C/m :
a/ D; A; E thẳng hàng
b/ \(DM\perp AB;EM\perp AC\)
c/ \(\Delta DME\) vuông
d/ EK // BC và EK =...
Đọc tiếp
Cho \(\Delta ABC;Â=90^0\) lấy các canh AB, AC là cạnh huyền dựng ra phía ngoài của \(\Delta ABC\) các \(\Delta\) vuông cân \(ADB\) và \(\Delta AEC\) . Gọi M là trung điểm của BC, DM cắt AB tại F, EM cắt AC tại K. C/m :
a/ D; A; E thẳng hàng
b/ \(DM\perp AB;EM\perp AC\)
c/ \(\Delta DME\) vuông
d/ EK // BC và EK = BC/2
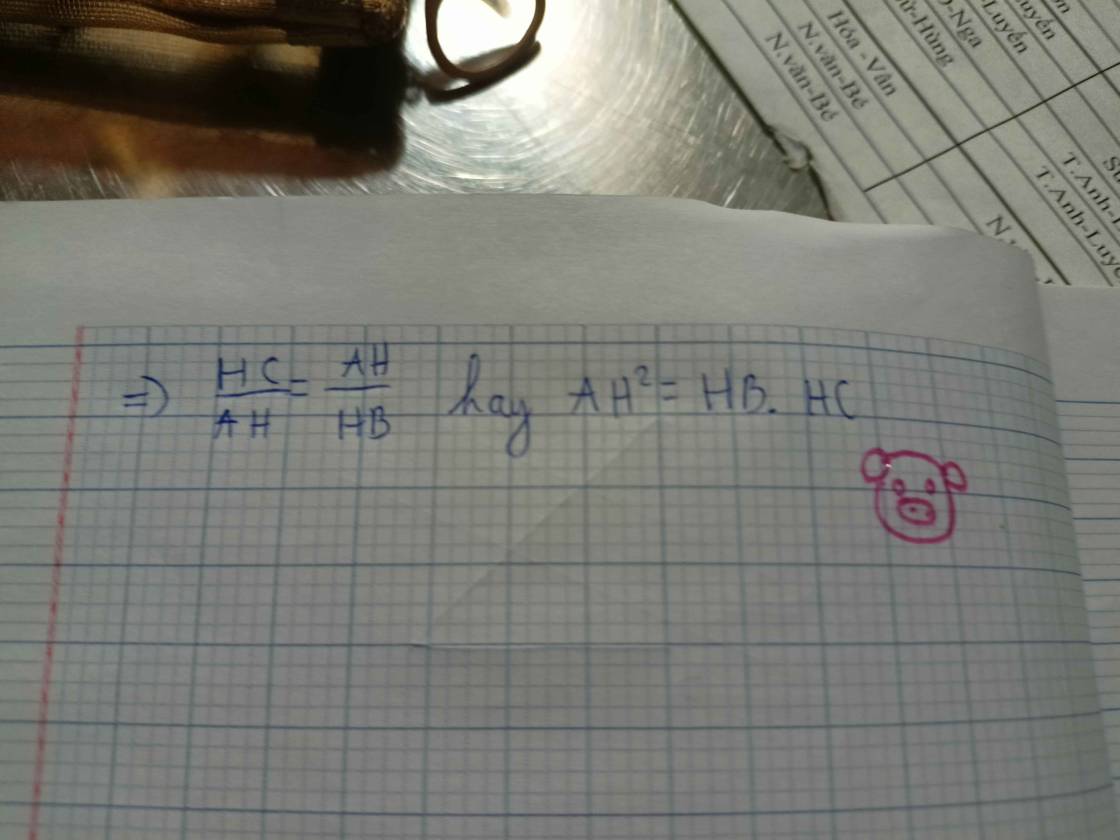
A B C D E M K
a) Vì ADB và AEC vuông cân tại D và E nên
DAB=EAC=45
Ta có:DAE=DAB+EAC+BAC
=45+45+90=180
=>D;A:E thẳng hàng(đpcm)
b)Vì AD=BD;EA=EC nên DM vàEm lần lượt là đường trung trực của cạnh AB;AC
Do đó:DM⊥AB;EM⊥AC(đpcm)
c,Vì DM⊥AB;EM⊥AC mà AB⊥AC nên EM⊥DM
=>tam giác DME vuông(đpcm)
d,S EK//BC nhỉ @@
À mà dạo này tôi bận lắm,vừa on thấy kèm tên nên ms giúp,lần sau chắc ko có thời gian làm giúp bn đc đâu
d, Nối tiếp bài bạn kia nha :v
\(\Delta ADB\) vuông cân tại D có DF là đường trung trực ( theo b ) => DF cũng là trung tuyến => FA = FB (1)
Tương tự, KA = KC (2)
Từ (1), (2) \(\Rightarrow FK\) là đường trung bình \(\Delta ABC\)
\(\Rightarrow\)FK // BC và \(FK=\dfrac{1}{2}BC\)
\(\Rightarrowđpcm\)
Không cm theo cách trên thì kẻ thêm: trên tia đối của FK lấy FH = FK rồi cm