giup em bai 1 voi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 11 2023
a, 8\(⋮\) \(x\); 12 \(⋮\) \(x\)
⇒ \(x\) \(\in\) ƯC(8; 12)
8 = 23; 12 = 22.3; ƯCLN(8; 12) = 22 = 4
\(x\) \(\in\) Ư(4) = {-4; - 2; -1; 1; 2; 4}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 11 2023
b, 120⋮ \(x\); 90 \(⋮\) \(x\)
⇒ \(x\) \(\in\) ƯC(120; 90)
120 = 23.3.5; 90 = 2.32.5; ƯCLN(120; 90) = 2.3.5 = 30
\(x\) \(\in\)Ư(30) = {-30; -15; -10; -6; - 5; -3; -2; -1; 1; 2; 3; 5;6; 10; 15; 30}
Vì - 5 < \(x\) < 10
Nên \(x\) \(\in\) {-3; -2; -1; 1; 2; 3; 5; 6}
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)
Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):
Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)
Do đó:
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
20 tháng 7 2023
Bài 3:
54 chia hết cho 18
38:18 = 2 (dư 2)
Vậy số tự nhiên a chia 18 được số dư là 2, thương là 14. Số tự nhiên a cần tìm là:
14 x 18 + 2 = 254
Đáp số: a là 254
HB
1
H9
HT.Phong (9A5)
CTVHS
6 tháng 12 2023
Bài 6:
a) n + 3 chia hết cho n - 1
⇒ n - 1 + 4 chia hết cho n - 1
⇒ 4 chia hết cho n - 1
⇒ n - 1 ∈ Ư(4) = {1; -1; 2; -2; 4; -4}
⇒ n ∈ {2; 0; 3; -1; 5; -3}
b) n - 3 chia hết cho n + 2
⇒ n + 2 - 5 chia hết cho n + 2
⇒ 5 chia hết cho n + 2
⇒ n + 2 ∈ Ư(5) = {1; -1; 2; -2}
⇒ n ∈ {-1; -3; 0; -4}
c) n - 5 chia hết cho n - 7
⇒ n - 7 + 2 chia hết cho n - 7
⇒ 2 chia hết cho n - 7
⇒ n - 7 ∈ Ư(2) = {1; -1; 2; -2}
⇒ n ∈ {8; 6; 9; 5}
d) n + 7 chia hết cho n - 4
⇒ n - 4 + 11 chia hết cho n - 4
⇒ 11 chia hết cho n - 4
⇒ n - 4 ∈ Ư(11) = {1; -1; 11; -11}
⇒ n ∈ {5; 3; 15; -7}
e) 3n - 1 chia hết cho n + 2
⇒ 3n + 6 - 7 chia hết cho n + 2
⇒ 3(n + 2) - 7 chia hết cho n + 2
⇒ 7 chia hết cho n + 2
⇒ n + 2 ∈ Ư(7) = {1; -1; 7; -7}
⇒ n ∈ {-1; -3; 5; -9}
f) 2n + 7 chia hết cho n - 1
⇒ 2n - 2 + 9 chia hết cho n - 1
⇒ 2(n - 1) + 9 chia hết cho n - 1
⇒ 9 chia hết cho n - 1
⇒ n - 1 ∈ Ư(9) = {1; -1; 3; -3; 9; -9}
⇒ n ∈ {2; 0; 4; -2; 10; -8}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 12 2023
Bài 5:
a, 3.55: (-5)4 + 5.(3\(x\) - 1) = 25
3.55 : 54 + 5.(3\(x\) - 1) = 25
3.5 + 5.(3\(x\) - 1) = 25
15 + 5.(3\(x\) - 1) = 25
5.(3\(x\) - 1) = 25 - 15
5.(3\(x\) -1) = 10
3\(x\) - 1 = 10 : 5
3\(x\) - 1 = 2
3\(x\) = 2 + 1
3\(x\) = 3
\(x\) = 3: 3
\(x\) = 1
ON
2
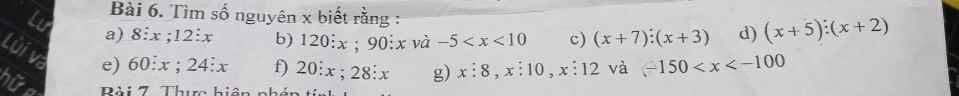
Trả lời:
Câu 1:
1, A = ( 2x - 3 )( 7x + 8 ) = 14x2 + 16x - 21x - 24 = 14x2 - 5x - 24
2, A = ( 3x + 7 )( x2 - 3x + 2 ) = 3x3 - 9x2 + 6x + 7x2 - 21x + 14 = 3x3 - 2x2 - 15x + 14
3, A = ( x2 - 2x + 5 )( x2 + x - 1 ) = x4 + x3 - x2 - 2x3 - 2x2 + 2x + 5x2 + 5x - 5 = x4 - x3 + 2x2 + 7x - 5
4, A = ( x2 - 3 )( x2 - 7x + 6 ) = x4 - 7x3 + 6x2 - 3x2 + 21x - 18 = x4 - 7x3 + 3x2 + 21x - 18
5, A = ( 2x - y )( 2x + y ) = 4x2 - y2
6, A = ( x - 2y )( x2 + 2xy + 4y2 ) = x3 - 8y3
7, A = ( x + 3y )( x2 - 3xy + 9y2 ) = x3 + 27y3
8, A = ( xy + 1 )( xy - 1 ) = x2y2 - 1