Cho tam giác ABC hãy xác định điểm S sao cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
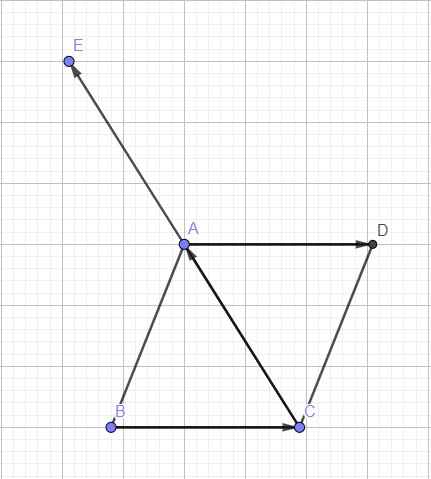
\(\overrightarrow{AD}=\overrightarrow{BC}\) \(\Rightarrow\) ABCD là hình bình hành
Vậy D là đỉnh của hình bình hành ABCD
\(\overrightarrow{AE}=\overrightarrow{CA}\Rightarrow\overrightarrow{AE}-\overrightarrow{CA}=\overrightarrow{0}\Rightarrow\overrightarrow{AE}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow A\) là trung điểm CE hay E là điểm đối xứng C qua A
CM
11 tháng 2 2019
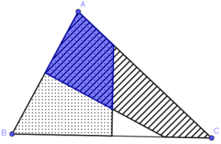
Áp dụng kết quả bài 70 (chương III – SGK) ta có:
MA < MB khi M thuộc nửa mặt phẳng chứa điểm A bờ là đường trung trực của AB (phần gạch chéo)
MB < MC khi M thuộc nửa mặt phẳng chứa điểm B bờ là đường trung trực của BC (phần được chấm chấm).
(Cách chứng minh xem lại bài 70).
Phần giao của hai nửa mặt phẳng trên là phần hình chứa điểm M thỏa mãn MA < MB < MC (phần hình được tô màu xanh).
CM
8 tháng 9 2018
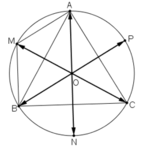
a)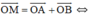 
M là đỉnh còn lại của hình bình hành AOBM.
+ AOBM là hình bình hành ⇒ AM = OB
Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)
+ AOBM là hình bình hành ⇒ AM//BO
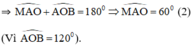
Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.
Mà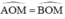 
nên M là điểm chính giữa cung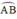 
b) Chứng minh tương tự phần a) ta có: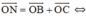 
N là điểm chính giữa cung BC.
c)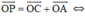 
P là điểm chính giữa cung CA.
17 tháng 1 2017
Nếu: +AB<AC
+AM+AB=AC
=>M nằm giữa A và B(Cách xác định điểm nằm giữa)
(Tick mình nha mình ko bít có đúng ko nhưng mình đã cố lắm rồi)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
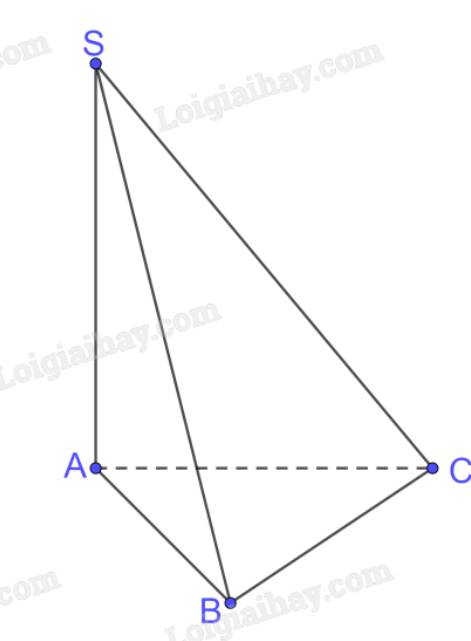
a) Ta có SA \( \bot \) (ABC) nên A là hình chiếu của S trên (ABC)
b) A là hình chiếu của S trên (ABC)
B là hình chiếu của B trên (ABC)
C là hình chiếu của C trên (ABC)
\( \Rightarrow \) Tam giác ABC là hình chiếu của tam giác SBC.
c) B là hình chiếu của C trên (SAB)
S, B là hình chiếu của chính nó trên (SAB)
\( \Rightarrow \) SB là hình chiếu của tam giác SBC trên (SAB)
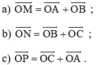
Lời giải:
Ta có:
\(5\overrightarrow{SA}-2\overrightarrow{SB}-\overrightarrow{SC}=\overrightarrow{0}\)
\(\Leftrightarrow 2\overrightarrow{SA}+2(\overrightarrow{SA}-\overrightarrow{SB})+(\overrightarrow{SA}-\overrightarrow{SC})=\overrightarrow{0}\)
\(\Leftrightarrow 2\overrightarrow{SA}+2\overrightarrow{BA}+\overrightarrow{CA}=\overrightarrow{0}\)
\(\Leftrightarrow 2(\overrightarrow {AS}+\overrightarrow{AB})+\overrightarrow{AC}=\overrightarrow{0}\)
Như vậy, ta có thể xác định điểm $S$ như sau:
Trên tia đối của tia $AC$ lấy điểm $R$ sao cho \(AR=\frac{AC}{2}\)
Khi đó, \(\overrightarrow{AC},\overrightarrow{AR}\) là các tia ngược hướng nhau nên \(\overrightarrow{AC}+2\overrightarrow{AR}=\overrightarrow{0}\)
Lấy điểm $S$ thỏa mãn \(ASRB\) là hình bình hành, khi đó, theo tính chất hình bình hành thì \(\overrightarrow{AB}+\overrightarrow{AS}=\overrightarrow{AR}\)
Như vậy, \(2(\overrightarrow{AS}+\overrightarrow{AB})+\overrightarrow{AC}=2\overrightarrow{AR}+\overrightarrow{AC}=\overrightarrow{0}\) , thỏa mãn đktđb
Vậy điểm $S$ xác định như trên là điểm cần tìm.