Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Khi x=25 thì A=(2*5)/(5+2)=10/7
2: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{x-4}=\dfrac{2\left(\sqrt{x}-2\right)}{x-4}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
3: căn x+2>=2
=>P<=2/2=1
Dấu = xảy ra khi x=0

a: =>x=13/52+8/52=21/52
b: =>x=1/36-27/36=-26/36=-13/18
c: =>x=24/60+15/60-20/60=19/60
d: =>x/15=9/15-10/15=-1/15
=>x=-1

a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé

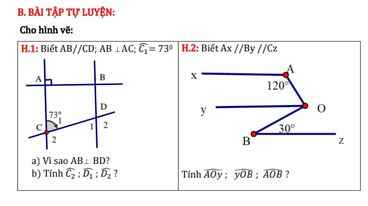
Hình 1:
a: Ta có: AC//BD
AB\(\perp\)AC
Do đó: BD\(\perp\)AB

Từ giả thiết, suy ra: \(\hat{M}=\dfrac{3}{2}\hat{P}\).
Ta có: \(\hat{D}+\hat{M}+\hat{P}=180^o\) (tổng 3 góc trong một tam giác)
\(\Leftrightarrow55^o+\dfrac{3}{2}\hat{P}+\hat{P}=180^o\Leftrightarrow\hat{P}=50^o\)
\(\Rightarrow\hat{M}=\dfrac{3}{2}\hat{P}=\dfrac{3}{2}\cdot50^o=75^o\)

\(=4\)
Cái này thì bạn rút gọn x - 1 thì còn \(\dfrac{-12}{-3}\)
Sau đó rút gọn -12 và -3 thì chỉ còn 4 thôi
=>(x-1)2 = -12 . (-3)
(x-1)2 = 36
(x-1)2 = 62 = (-6)2
*) x-1=6 *) x-1=-6
x=7 x=-5
=>x thuộc (7,-5)

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)

\(x^4-4x^2+x^2-4x=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x\left(x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-4x+x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\)
hay x=0
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^3-3x-4=0\end{matrix}\right.\\ \Leftrightarrow x=0\)

refer
Đặc điểm tổ chức quân đội thời Lê Sơ:
-Thực hiện chính sách Ngụ binh ư nông.
- Quân đội gồm 2 bộ phận: Quân triều đình và Quân địa phương: bộ binh,thủy binh,tượng và nghị binh.
-Vũ khí: đao,kiếm,cung tên,hỏa đồng,hỏa pháo. Kiên quyết bảo vệ vùng biên giới Tổ quốc.
Đặc điểm tổ chức quân đội thời Trần:
-Quân đội tuyển chọn theo chính sách "ngụ binh ư nông", "quân lính cốt tinh nhuệ,không cốt đông". Học tập binh pháp và luyện tập võ nghệ.
-Bố trí tướng giỏi đóng quân ở các vùng hiểm yếu. Nhất là vùng biên giới phía Bắc.
Giống nhau:
-Đều tuyển chọn theo chính sách "ngụ binh ư nông".
-Đề cao giữ gìn và bảo vệ chủ quyền quốc gia.
Khác nhau:
-Thời Lê Sơ:
+ Bộ máy tố chức quân đội gồm 2 bộ phận.(Có sự sắp đặt)
+ Vũ khí đa dạng,sắt bén.
-Thời Trần:
+ Bộ máy tổ chức quân đội không có sự sắp đặt.
+ Vũ khí thô sơ: cuốc,cày,.....
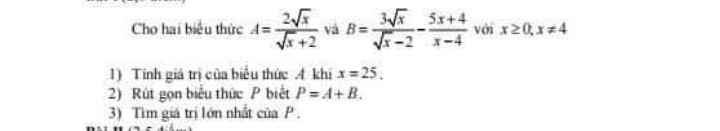

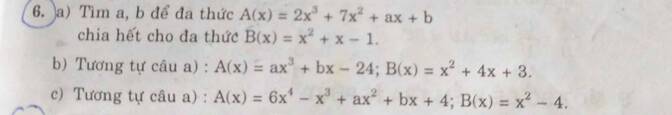
 giúp mik giải bài toán hình 7 này với ạ
giúp mik giải bài toán hình 7 này với ạ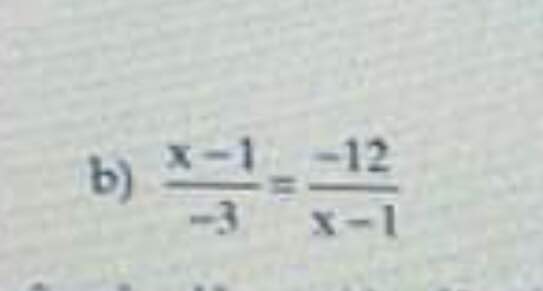

 Giải giúp mik bài này ạ!Thanks...
Giải giúp mik bài này ạ!Thanks...
a, Xét tam giác AHB và tam giác CHA ta có :
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác AHB ~ tam giác CHA ( g.g )
\(\frac{AH}{HC}=\frac{HB}{AH}\Rightarrow AH^2=HB.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{256}{25}\)cm
\(\Rightarrow BC=BH+HC=25+\frac{256}{25}=\frac{881}{25}\)cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=\sqrt{881}\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=18,99...\)cm
b, Theo định lí Pytago tam giác AHB vuông tại H
\(AH=\sqrt{AB^2-BH^2}=6\sqrt{3}\)cm
Do tam giác AHB ~ tam giác CHA ( cma )
\(\frac{AH}{CH}=\frac{HB}{AH}\Rightarrow AH^2=HB.HC\Rightarrow HC=\frac{AH^2}{HB}=18\)cm
\(\Rightarrow BC=BH+HC=6+18=24\)cm
Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12\sqrt{3}\)cm