Biết sin.cos = 0,48. Tinh \(sin^3+cos^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
29 tháng 7 2018
ta có : \(sinx-cosx=\dfrac{1}{3}\Leftrightarrow sin^2x+cos^2x-2sinx.cosx=\dfrac{1}{9}\)
\(\Leftrightarrow-sinx.cosx=\dfrac{-4}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}sinx-cosx=\dfrac{1}{3}\\sinx\left(-cos\right)=\dfrac{-4}{9}\end{matrix}\right.\)
sử dụng vi ét đảo \(\Rightarrow\) \(sinx\) và \(-cosx\) là nghiệm của phương trình :
\(X^2-\dfrac{1}{3}X-\dfrac{4}{9}\) \(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}sinx=\dfrac{1+\sqrt{17}}{6}\\-cosx=\dfrac{1-\sqrt{17}}{6}\end{matrix}\right.\\\left\{{}\begin{matrix}sinx=\dfrac{1-\sqrt{17}}{6}\\-cosx=\dfrac{1+\sqrt{17}}{6}\end{matrix}\right.\end{matrix}\right.\)
từ đó \(\Rightarrow\) \(sinx\overset{.}{,}cosx\) rồi thế vào các bài toán bấm máy là ra .
NH
1
29 tháng 8 2018
ta có : \(\left(sin\alpha+cos\alpha\right)^2=1+2sin\alpha.cos\alpha=\dfrac{49}{25}\)
\(\Rightarrow sin\alpha+cos\alpha=\pm\dfrac{7}{5}\)
ta có : \(A=sin^3\alpha+cos^3\alpha=\left(sin\alpha+cos\alpha\right)^3-3sin\alpha.cos\alpha\left(sin\alpha+cos\alpha\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}A=\left(\dfrac{7}{5}\right)^3-3\left(0,48\right)\left(\dfrac{7}{5}\right)=\dfrac{91}{125}\\A=\left(\dfrac{-7}{5}\right)^3-3\left(0,48\right)\left(\dfrac{-7}{5}\right)=\dfrac{-91}{125}\end{matrix}\right.\)
vậy \(sin^3\alpha+cos^3\alpha=\pm\dfrac{91}{125}\)
29 tháng 8 2018
hình như bạn nhầm r ạ sao lại 49/25 ạ hoặc là mk chưa hiểu
NN
1
28 tháng 7 2018
ta có : \(sin^2x+cos^2x=1\Leftrightarrow\left(sinx+cosx\right)^2-2sinx.cosx=1\)
\(\Leftrightarrow\left(sinx+cosx\right)^2-0,96=1\) \(\Leftrightarrow sinx+cosx=\pm\sqrt{1,96}=\pm1,4\)
ta có : \(sin^3x+cos^3x=\left(sinx+cosx\right)^3-3sinx.cosx\left(sinx+cosx\right)\)
th1: \(sinx+cosx=1,4\Rightarrow sin^3x+cos^3x=0,728\)
th2: \(sinx+cosx=-1,4\Rightarrow sin^3x+cos^3x=-0,728\)
vậy ............................................................................................................
TV
9 tháng 10 2016
a) sin anpha = 2/3 => góc anpha = 42o
cos 42o = 0,743
tan 42o = 0,9
cot 42o = 1/tan 42o = 1/0,9 = 1,111
b) tan anpha + cot anpha = 3
<=> tan anpha + 1/tan anpha = 3
<=> tan2 anpha = 2
<=> tan anpha = \(\sqrt{2}\)
=> góc anpha = 55o
Ta có: a = sin 55o . cos 55o
<=> a = 0,469
4 tháng 4 2019
Có : ΔABC vuông tại A => sinB = cosC = \(\frac{3}{4}\)
Mà lại có : sin2 B + cos2B = 1
=> cos2B = 1 - sin2B
=> cosB = 1 - \(\frac{3}{4}\)= \(\frac{1}{4}\)
17 tháng 8 2018
ta có : \(A=\dfrac{sin^3\alpha+cos^3\alpha}{2sin\alpha.cos^2\alpha+cos^2\alpha.sin^2\alpha}\)
\(\Leftrightarrow A=\dfrac{\dfrac{sin^3\alpha}{cos^3\alpha}+\dfrac{cos^3\alpha}{cos^3\alpha}}{\dfrac{2sin\alpha.cos^2\alpha}{cos^3\alpha}+\dfrac{cos\alpha.sin^2\alpha}{cos^3\alpha}}=\dfrac{tan^3\alpha+1}{2tan\alpha+tan^2\alpha}\)
\(\Leftrightarrow A=\dfrac{\left(\dfrac{3}{4}\right)^3+1}{2\left(\dfrac{3}{4}\right)+\left(\dfrac{3}{4}\right)^2}=\dfrac{91}{132}\)
NT
0
TQ
1
PN
3 tháng 10 2017
VT = sin3a.cos^3a + sin^3a.cos3a
= sin3a.cosa.cos^2a + sin^2a.sina.cos3a
= 1/2.(sin2a + sin4a).cos^2a + 1/2.sin^2a.(sin(-2a) + sin4a)
= 1/2.(sin2a + sin4a).cos^2a + 1/2.sin^2a.(sin4a - sin2a)
= 1/2.sin2a.cos^2a + 1/2.sin4a.cos^2a + 1/2.sin^2a.sin4a - 1/2.sin^2a.sin2a
= 1/2.sin2a.(cos^2a - sin^2a) + 1/2.sin4a.(cos^2a + sin^2a)
= 1/2.sin2a.cos2a + 1/2.sin4a
= 1/4.sin4a + 1/2.sin4a
= 3/4.sin4a = VP
=> đpcm
P/s: Chỉ sợ you ko hiểu
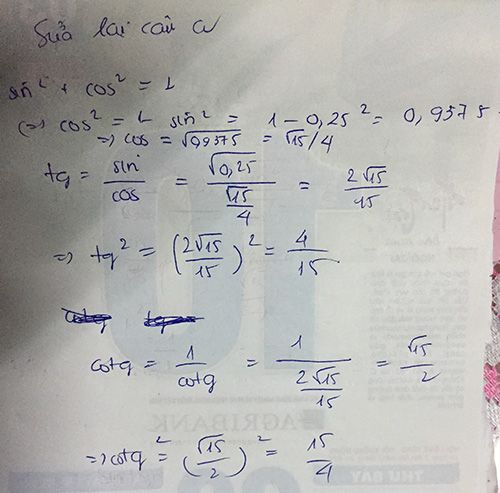
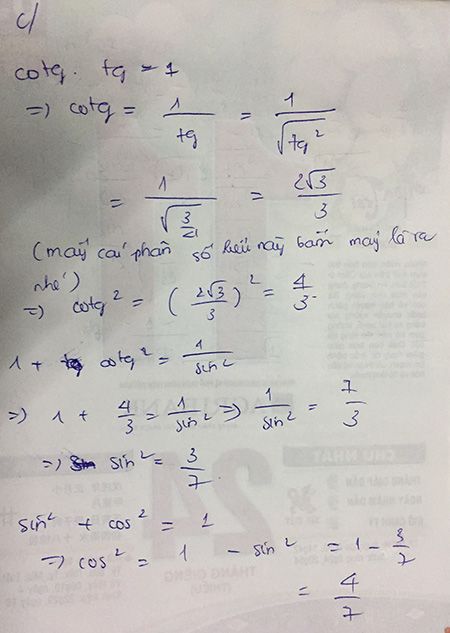
Ai giúp mk vs ạ. Đang cần gấp. Cảm ơn