Mọi ng ơi giúp mk vs, câu c, câu d nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
1
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
a.
\(\Leftrightarrow\dfrac{2a}{2a+b}+\dfrac{2b}{2b+c}+\dfrac{2c}{2c+a}\le2\)
\(\Leftrightarrow\dfrac{2a}{2a+b}-1+\dfrac{2b}{2b+c}-1+\dfrac{2c}{2c+a}-1\le-1\)
\(\Leftrightarrow\dfrac{b}{2a+b}+\dfrac{c}{2b+c}+\dfrac{a}{2c+a}\ge1\)
Thật vậy, ta có:
\(VT=\dfrac{b^2}{2ab+b^2}+\dfrac{c^2}{2bc+c^2}+\dfrac{a^2}{2ca+a^2}\ge\dfrac{\left(a+b+c\right)^2}{a^2+b^2+c^2+2ab+2bc+2ca}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
b.
Chuẩn hóa \(a+b+c=1\), BĐT cần chứng minh trở thành:
\(\dfrac{a}{\left(a+2b\right)^2}+\dfrac{b}{\left(b+2c\right)^2}+\dfrac{c}{\left(c+2a\right)^2}\ge1\)
Ta có:
\(\dfrac{a}{\left(a+2b\right)^2}+a\left(a+2b\right)+a\left(a+2b\right)\ge3a\)
Tương tự:
\(\dfrac{b}{\left(b+2c\right)^2}+b\left(b+2c\right)+b\left(b+2c\right)\ge3b\)
\(\dfrac{c}{\left(c+2a\right)^2}+c\left(c+2a\right)+c\left(c+2a\right)\ge3c\)
Cộng vế:
\(VT+2\left(a+b+c\right)^2\ge3\left(a+b+c\right)\)
\(\Leftrightarrow VT+2\ge3\)
\(\Leftrightarrow VT\ge1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
CC
0
CC
1
5 tháng 4 2018
CN VN
a)Người thanh niên ấy/làm mọi người khó chịu
C V
CN VN
b)Sự năng nổ học tập của Lan/khiến mọi người ngạc nhiên
C V
CN VN
c)Cuốn sách có nhiều tranh/ minh họa
C V
CN VN
đ)Mẹ biết được điểm 10 /là một sự tiến bộ
C V
CHÚC BẠN HỌC TỐT !!! nhớ k cho mk nha
ML
12 tháng 7 2023
a/ ĐKXĐ: 2x - 1 >= 0 <=> 2x > 1 <=> x>= 1/2
\(\sqrt{2x-1}=\sqrt{5}\Leftrightarrow2x-1=5\Leftrightarrow2x=6\Leftrightarrow x=3\left(tm\right)\)
b/ ĐKXĐ: x - 10 >= 0 <=> x >= 10
Biểu thức trong căn luôn nhận giá trị dương => vô nghiệm
c/ ĐKXĐ: x - 5 >=0 <=> x >= 5
\(\sqrt{x-5}=3\Leftrightarrow x-5=9\Leftrightarrow x=14\left(tm\right)\)
H9
HT.Phong (9A5)
CTVHS
12 tháng 7 2023
a) \(\sqrt{2x-1}=\sqrt{5}\) (ĐK: \(x\ge\dfrac{1}{2}\))
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=3\left(tm\right)\)
b) \(\sqrt{x-10}=-2\)
⇒ Giá trị của biểu thức trong căn luôn dương nên phương trình vô nghiệm
c) \(\sqrt{\left(x-5\right)^2}=3\)
\(\Leftrightarrow\left|x-5\right|=3\)
TH1: \(\left|x-5\right|=x-5\) với \(x-5\ge0\Leftrightarrow x\ge5\)
Pt trở thành:
\(x-5=3\) (ĐK: \(x\ge5\))
\(\Leftrightarrow x=3+5\)
\(\Leftrightarrow x=8\left(tm\right)\)
TH2: \(\left|x-5\right|=-\left(x-5\right)\) với \(x-5< 0\Leftrightarrow x< 0\)
Pt trở thành:
\(-\left(x-5\right)=3\) (ĐK: \(x< 5\))
\(\Leftrightarrow-x+5=3\)
\(\Leftrightarrow-x=-2\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(S=\left\{2;8\right\}\)
7 tháng 1 2018
2 câu tiếp theo :
Em nghe em về quê hương ngay
Em đã sáng tác hết đây này
7 tháng 7 2023
2:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH=12cm
b: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
c: góc IAC+góc AED
=góc ICA+góc AHD
=góc ACB+góc ABC=90 độ
=>AI vuông góc ED
4:
a: góc BDH=góc BEH=góc DBE=90 độ
=>BDHE là hình chữ nhật
b: BDHE là hình chữ nhật
=>góc BED=góc BHD=góc A
Xét ΔBED và ΔBAC có
góc BED=góc A
góc EBD chung
=>ΔBED đồng dạng với ΔBAC
=>BE/BA=BD/BC
=>BE*BC=BA*BD
c: góc MBC+góc BED
=góc C+góc BHD
=góc C+góc A=90 độ
=>BM vuông góc ED
A
1
TH
11
28 tháng 5 2019
123456789 + 987654321 = 1111111110
Ê béo gửi câu hỏi đàng hoàng chút đi
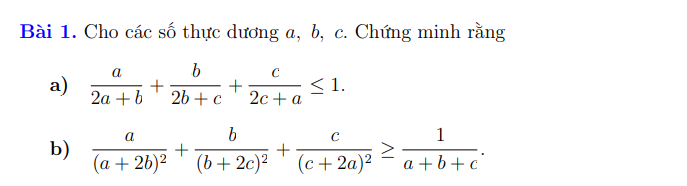
a) \(\left(3\sqrt{27}-2\sqrt{75}+\sqrt{363}\right)\sqrt{3}=3\sqrt{81}-2\sqrt{225}+\sqrt{1089}\)
\(=3.9-2.15+33=27-30+33=30\)
b) \(\left(12\sqrt{2}-3\sqrt{18}+2\sqrt{8}\right):\sqrt{2}=12-3\sqrt{9}+2\sqrt{4}\)
\(=12-3.3+2.2=12-9+4=7\)
c) \(\sqrt{7-2\sqrt{10}}+\sqrt{20}+\dfrac{1}{2}\sqrt{8}=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}+2\sqrt{5}+\sqrt{2}\)
\(=\left|\sqrt{5}-\sqrt{2}\right|+2\sqrt{5}+\sqrt{2}=\sqrt{5}-\sqrt{2}+2\sqrt{5}+\sqrt{2}=3\sqrt{5}\)
d) \(\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}=\dfrac{\sqrt{2}\sqrt{3-\sqrt{5}}}{\sqrt{2}}-\dfrac{\sqrt{2}\sqrt{3+\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{2\left(3-\sqrt{5}\right)}}{\sqrt{2}}-\dfrac{\sqrt{2\left(3+\sqrt{5}\right)}}{\sqrt{2}}=\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}-\dfrac{\sqrt{6+2\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}}{\sqrt{2}}-\dfrac{\sqrt{\left(\sqrt{5}+1\right)^2}}{\sqrt{2}}=\dfrac{\left|\sqrt{5}-1\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+1\right|}{\sqrt{2}}\)
\(=\dfrac{\sqrt{5}-1}{\sqrt{2}}-\dfrac{\sqrt{5}+1}{\sqrt{2}}=\dfrac{\sqrt{5}-1-\left(\sqrt{5}+1\right)}{\sqrt{2}}=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}\)
\(=\dfrac{-2}{\sqrt{2}}=\dfrac{-\sqrt{2}.\sqrt{2}}{\sqrt{2}}=\dfrac{-\sqrt{2}}{1}=-\sqrt{2}\)