1.Phân tích các đa thức sau thành nhân tử
a, x2+7x+10
b,x2-3x+2
c, x2-5x-24
d, 2x2-10x+12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2021
\(a,=\left(x+1\right)\left(x+3\right)\\ b,=-5x^2+15x+x-3=\left(x-3\right)\left(1-5x\right)\\ c,=2x^2+2x+5x+5=\left(2x+5\right)\left(x+1\right)\\ d,=2x^2-2x+5x-5=\left(x-1\right)\left(2x+5\right)\\ e,=x^3+x^2-4x^2-4x+x+1=\left(x+1\right)\left(x^2-4x+1\right)\\ f,=x^2+x-5x-5=\left(x+1\right)\left(x-5\right)\)
CM
25 tháng 12 2018
a) (x - y)(x + y + 3). b) (x + y - 2xy)(2 + y + 2xy).
c) x 2 (x + l)( x 3 - x 2 + 2). d) (x – 1 - y)[ ( x - 1 ) 2 + ( x - 1 ) y + y 2 ].
16 tháng 8 2021
casio fx 570 thì ấn mode => 5 => 3 sau điền hệ số a;b;c
casio fx 580 thì ấn mode => 9 => 2 => 2 => điền hệ số a;b;c
16 tháng 8 2021
có cả cách này à =)))
menu setup -> 9 -> 2 - > 2 (pt cần phân tích) -> nhập hệ số của pt vào từng biến thích hợp -> ''=''
VD : \(A=x^2+4x-5\)có nghiệm \(x_1=1;x_2=-5\)
vậy đa thức cần phân tích là : \(\left(x-1\right)\left(x+5\right)=x^2+5x-x-5\)
Vậy \(A=x^2+4x-5=x^2+5x-x-5=\left(x-1\right)\left(x+5\right)\)
tương tự nhé
CM
24 tháng 9 2019
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
a) x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
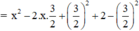
(Vì có x2 và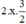 
nên ta thêm bớt 
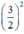để xuất hiện HĐT)
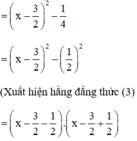
= (x – 2)(x – 1)
b) x2 + x - 6
= (x – 2)(x + 3).
c) x2 + 5x + 6
= (x + 2)(x + 3).
CM
19 tháng 1 2017
a) (x - 2)(x - 3). b) 3(x - 2)(x + 5).
c) (x - 2)(3x + 1). d) (x-2y)(x - 5y).
e) (x + l)(x + 2)(x - 3). g) (x-1)(x + 3)( x 2 + 3).
h) (x + y - 3)(x - y + 1).
KV
9 tháng 12 2023
Bài 3
a) x² + 10x + 25
= x² + 2.x.5 + 5²
= (x + 5)²
b) 8x - 16 - x²
= -(x² - 8x + 16)
= -(x² - 2.x.4 + 4²)
= -(x - 4)²
c) x³ + 3x² + 3x + 1
= x³ + 3.x².1 + 3.x.1² + 1³
= (x + 1)³
d) (x + y)² - 9x²
= (x + y)² - (3x)²
= (x + y - 3x)(x + y + 3x)
= (y - 2x)(4x + y)
e) (x + 5)² - (2x - 1)²
= (x + 5 - 2x + 1)(x + 5 + 2x - 1)
= (6 - x)(3x + 4)
KV
9 tháng 12 2023
Bài 4
a) x² - 9 = 0
x² = 9
x = 3 hoặc x = -3
b) (x - 4)² - 36 = 0
(x - 4 - 6)(x - 4 + 6) = 0
(x - 10)(x + 2) = 0
x - 10 = 0 hoặc x + 2 = 0
*) x - 10 = 0
x = 10
*) x + 2 = 0
x = -2
Vậy x = -2; x = 10
c) x² - 10x = -25
x² - 10x + 25 = 0
(x - 5)² = 0
x - 5 = 0
x = 5
d) x² + 5x + 6 = 0
x² + 2x + 3x + 6 = 0
(x² + 2x) + (3x + 6) = 0
x(x + 2) + 3(x + 2) = 0
(x + 2)(x + 3) = 0
x + 2 = 0 hoặc x + 3 = 0
*) x + 2 = 0
x = -2
*) x + 3 = 0
x = -3
Vậy x = -3; x = -2
8 tháng 10 2021
\(a,=\left(x-2\right)^2-y^2=\left(x-y-2\right)\left(x+y-2\right)\\ b,=4x^2\left(x^2+2x+1\right)=4x^2\left(x+1\right)^2\\ c,=xy^2\left(x^2-2xy+y^2\right)=xy^2\left(x-y\right)^2\\ d,=\left(x-y\right)\left(x+y\right)-7\left(x-y\right)=\left(x-y\right)\left(x+y-7\right)\\ e,=\left(5x-2y\right)\left(5x+2y\right)\\ f,=x^2+3x+4x+12=\left(x+3\right)\left(x+4\right)\\ i,=x^2+2x-7x-14=\left(x+2\right)\left(x-7\right)\)
22 tháng 12 2021
a) \(=x\left(x-5\right)\)
b) \(=\left(x+3y-3y\right)\left(x+3y+3y\right)=x\left(x+6y\right)\)
c) \(=x\left(x+y\right)-3\left(x+y\right)=\left(x+y\right)\left(x-3\right)\)
16 tháng 8 2021
a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)
b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)
d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)
e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)
d.
= 2x\(^2\)-4x-6x+12
=2x(x-2)-6(x-2)
=(2x-6)(x-2)
a.
= \(x^2\)+2x+5x+10
=x(x+2) +5(x+2)
=(x+5)(x+2)